La energía cinética rotacional es una forma de energía cinética que se presenta cuando un objeto gira alrededor de un eje. Al igual que con la energía cinética lineal, donde la energía está relacionada con el movimiento lineal, la energía cinética rotacional está asociada con el movimiento de rotación.
Ejemplos prácticos
- Ruedas de Vehículos: Cuando un vehículo se mueve, las ruedas giran alrededor de su eje, lo que es un ejemplo clásico de un sistema en rotación.
- Movimiento de la Tierra: La rotación de la Tierra alrededor de su propio eje y su movimiento alrededor del Sol son ejemplos de sistemas en rotación en astronomía.

Cálculo de Radianes (Necesario para entender las fórmulas)
Calcular radianes es bastante sencillo una vez que entiendes la relación entre radianes y grados. Aquí tienes una explicación rápida:
- Entiende la relación básica: Un círculo completo tiene 360° en grados o 2π radianes. Esto significa que 360° es igual a 2π radianes.
- Convierte de grados a radianes: Si tienes un ángulo en grados y quieres convertirlo a radianes, usa la fórmula:

- Convierte de radianes a grados: Si tienes un ángulo en radianes y quieres convertirlo a grados, usa la fórmula:

Por ejemplo, si quieres convertir 90 grados a radianes, harías lo siguiente:

Y si quieres convertir π radianes a grados, sería:

Ecuaciones Básicas de Rotación
Desplazamiento Angular (θ)
El desplazamiento angular es una medida del ángulo a través del cual un objeto ha girado. Se expresa comúnmente en radianes o grados.
Ejemplo Práctico: Si una rueda da una vuelta completa, su desplazamiento angular es de 2π radianes.
Velocidad Angular (ω)
La velocidad angular describe qué tan rápido cambia el desplazamiento angular de un objeto en rotación.
Ejemplo Práctico: Si una rueda gira más rápido, su velocidad angular aumenta. Esta se puede medir tomando el cambio en el desplazamiento angular durante un intervalo de tiempo.
Aceleración Angular (α)
Representa el cambio en la velocidad angular. Una aceleración angular positiva significa que un objeto está girando más rápido, mientras que una aceleración negativa (desaceleración) indica que está disminuyendo su velocidad de rotación.
Ejemplo Práctico: Al aplicar frenos en una rueda giratoria, la aceleración angular es negativa ya que la velocidad de rotación disminuye.
Trabajo Rotacional
El trabajo rotacional es similar al trabajo lineal, pero en lugar de fuerza y desplazamiento, involucra torque y desplazamiento angular.
Torque (τ)
El torque, también conocido como momento de fuerza, es una medida de la tendencia de una fuerza a hacer girar un objeto alrededor de un eje, fulcro o punto de pivote. Matemáticamente, el torque se define como el producto cruz de la distancia (r) desde el punto de aplicación de la fuerza hasta el eje de rotación y la fuerza (F) aplicada. Se expresa mediante la fórmula:

Donde:
- τ es el torque.
- r es la distancia desde el punto de aplicación de la fuerza hasta el eje de rotación.
- F es la magnitud de la fuerza aplicada.
El torque es una cantidad vectorial, lo que significa que tiene tanto magnitud como dirección. La dirección del torque depende de la dirección en la que la fuerza tiende a hacer girar el objeto.
Ejemplos de Torque
- Apretando una Tuerca con una Llave: Si se desea apretar una tuerca con una llave, la forma más efectiva de generar el máximo torque es aplicar la fuerza lo más alejado posible de la cabeza de la llave. Esto se debe a que el torque es directamente proporcional a la distancia desde el punto de aplicación de la fuerza hasta el eje de giro. Al aplicar la fuerza en el extremo más lejano de la llave, se maximiza la distancia r, aumentando así el torque generado.
- Abrir una Puerta: Al abrir una puerta, se aplica una fuerza cerca del borde de la puerta, lejos de las bisagras, para generar un torque suficiente que permita girar la puerta con facilidad. Si se intentara abrir la puerta aplicando fuerza cerca de las bisagras (el eje de rotación), se necesitaría mucha más fuerza para generar el mismo torque.
- Subir una Bandera: En un mástil de bandera, el torque necesario para subir la bandera es generado por la fuerza aplicada en la manivela. Aquí, el radio de la manivela determina la distancia r, y la fuerza aplicada en la manivela genera el torque necesario para vencer la resistencia de la bandera y el peso del mecanismo.

Energía Cinética Rotacional
La energía cinética en sistemas rotativos depende del momento de inercia, que es el equivalente rotacional de la masa en el movimiento lineal.
Momento de Inercia (I)
El momento de inercia es una medida de la resistencia de un objeto a cambiar su estado de rotación. Es el equivalente rotacional de la masa en el movimiento lineal. Cuanto mayor es el momento de inercia, más difícil es cambiar la velocidad angular del objeto, ya sea acelerando o desacelerando. Ejemplo Práctico: Un disco sólido y un aro con la misma masa, pero diferente distribución de la misma tendrán diferentes momentos de inercia.
En sistemas rotacionales, el momento de inercia juega un papel crucial en determinar cómo se comporta un objeto bajo la influencia de un torque aplicado. Por ejemplo, en un carrusel, los caballos más alejados del centro (eje de rotación) contribuyen más al momento de inercia total que aquellos más cercanos al centro. Esto significa que se necesitará más fuerza para cambiar la velocidad de rotación del carrusel.
Ecuación del Momento de Inercia
La ecuación general del momento de inercia para un objeto de masa (m) que rota alrededor de un eje es:

donde I es el momento de inercia, ri es la distancia del elemento de masa mi al eje de rotación. Esta es una ecuación sumatoria, indicando que el momento de inercia es la suma de todos los productos de la masa y el cuadrado de su distancia al eje de rotación para cada punto de masa en el objeto.
La ecuación para una masa puntual es (la más importante para el EXANI-II):

Momentos de Inercia de Diversos Cuerpos Homogéneos
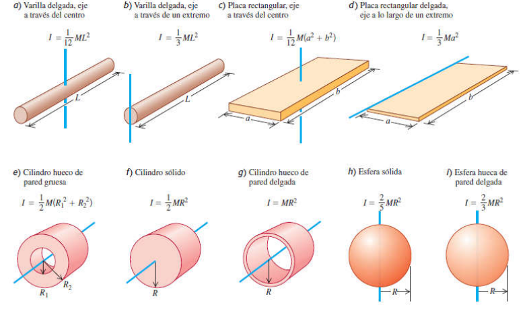
Fórmulas y Ecuaciones
Trabajo Rotacional
El trabajo realizado por un torque en un sistema rotativo se define como:

donde W es el trabajo, τ es el torque, y θ es el desplazamiento angular en radianes.
Energía Cinética Rotacional
La energía cinética rotacional es la energía debido al movimiento de rotación de un objeto. La fórmula es:

donde Krot es la energía cinética rotacional, I es el momento de inercia, y ω es la velocidad angular.
Reestructuración de Fórmulas para Facilitar su Aplicación
Trabajo Rotacional: Para simplificar la aplicación de la fórmula del trabajo rotacional, podemos relacionar el torque con la fuerza aplicada y la distancia al eje de rotación:

Entonces,

donde r es el brazo de palanca y F es la fuerza aplicada.
Energía Cinética Rotacional: Para objetos con formas geométricas simples, se pueden usar las fórmulas específicas del momento de inercia mencionadas anteriormente. Por ejemplo, para un disco sólido:

Sustituyendo esto en la ecuación de energía cinética rotacional, obtenemos:

Relación entre Desplazamiento Angular y Velocidad Lineal
La relación entre desplazamiento angular (en radianes) y velocidad lineal (v) es:

donde r es el radio de la trayectoria circular y ω es la velocidad angular. Esto muestra cómo la velocidad lineal en el borde de un objeto rotativo está directamente relacionada con su velocidad angular.
Ejercicios EXANI-II
Ejemplo 1 (Ejercicio tomado del EXANI-II):
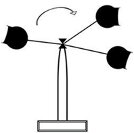
Para medir la velocidad del viento se construye un aparato de 3 copas, como el que se muestra en la imagen. Si cada copa tiene una masa de 0.2 kg y las varillas, de masa despreciable, tienen una longitud de 0.5 m, ¿cuál es el momento de inercia cuando el sistema rota?
- 0.05 kg·m2
- 0.10 kg·m2
- 0.15 kg·m2
Resolución:
El momento de inercia (I) de un sistema de partículas se define como la suma de los productos de las masas de las partículas y el cuadrado de sus distancias al eje de rotación. Matemáticamente se expresa como:

donde mi es la masa de la i-ésima partícula y ri es la distancia de la i-ésima partícula al eje de rotación.
En el caso de este ejercicio, tenemos un aparato con tres copas idénticas montadas en varillas de masa despreciable. Esto significa que solo necesitamos considerar la masa de las copas para calcular el momento de inercia. La fórmula para el momento de inercia de cada copa, que se puede modelar como una masa puntual al final de una varilla sin masa, es simplemente m*r².
Dado que las tres copas y varillas son idénticas, el momento de inercia total del sistema será tres veces el momento de inercia de una de las copas. Entonces:

Donde m es la masa de una copa y r es la longitud de la varilla.
Dado que la masa m es 0.2 kg y la longitud r es 0.5 m, podemos sustituir estos valores en la fórmula para obtener:

Vamos a calcular esto.
El momento de inercia del sistema cuando rota es de 0.15kg*m². Por lo tanto, la respuesta correcta es: c) 0.15kg*m²
🚀 ¡Potencia tu Preparación con Nuestro Plan Profesional! 🎓
Si has empezado a descubrir cómo prepararte para el EXANI-II con nuestro contenido gratuito, ¡te felicitamos! 🌟 Pero, ¿estás listo para dar el gran salto? Con nuestro Plan Profesional, no solo vas un paso adelante, ¡vas a volar! 🚀
Al elegir el Plan Profesional, desbloquearás acceso a:
- Contenido sin Publicidad y sin Interrupciones 🚫: Estudia con la máxima concentración, sin anuncios que te distraigan de tus objetivos.
- Contenido de Calidad 100% Basado en las Guías del EXANI-II 📚: Confía en un material que sigue fielmente el currículo oficial, maximizando tu eficacia en el estudio.
- Lecciones Escritas y Videos Explicativos 📝🎥: Visualiza conceptos complejos con materiales diseñados para facilitar tu aprendizaje.
- Explicaciones Paso a Paso 📘: Todo se entiende mejor con nuestros métodos sencillos y claros.
- Preguntas Como en el Examen ❓: Practica con ejercicios que te preparan de verdad, aumentando tu seguridad al máximo.
- Simuladores de Examen 💻: Siente el día del examen antes de llegar, para que nada te sorprenda.
- Acceso Multiplataforma 📱💻: Aprende cuando quieras y desde cualquier dispositivo, facilitando tu preparación en todo momento.
Asegura tu acceso al éxito con el Plan Profesional. No es solo preparación, es tu boleto para lograr tus sueños universitarios. ¡Decídete ya! 🌈 No dejes pasar esta oportunidad. ⏳ ¡El tiempo vuela y tu futuro te espera!
🌟 Simulador Gratis 🌟
Si estás curioso sobre lo que el Plan Profesional puede ofrecerte, te tenemos una sorpresa. Haz clic aquí y enfrenta nuestro simulador especial. Con solo 30 preguntas, podrás medir qué tan preparado estás para tu examen de admisión. 🎯
Esta es tu oportunidad de obtener un vistazo de la calidad y profundidad que nuestro Plan Profesional tiene para ofrecer, y al mismo tiempo, evaluar tu nivel actual de preparación. 💪

