Resolviendo el Simulador del EXANI-II de Física del Ceneval

El módulo de Física en el EXANI-II es uno de los más desafiantes, ya que integra conceptos que combinan teoría y aplicación práctica en problemas de la vida real. Este simulador gratuito está diseñado para ponerte en las mismas condiciones del examen real, ayudándote a reconocer tu nivel de dominio, identificar áreas de mejora y practicar bajo presión controlada.

Las preguntas están clasificadas por tema, lo que te permitirá identificar de inmediato a qué área pertenece cada reactivo. Algunos de estos temas estarán disponibles gratis, mientras que otros requieren el acceso al curso completo de Pasatuexam, donde encontrarás explicaciones detalladas, ejemplos resueltos y tips para dominar la sección.

---

¿Qué mide este simulador de Física?

Este simulador pone a prueba tu capacidad de aplicar conceptos físicos en situaciones concretas. Entre los temas que cubre se encuentran:

• Cinemática y dinámica: Leyes de Newton, planos inclinados, fuerzas y fricción.
• Trabajo, energía y potencia: Energía cinética, potencial y conservación de la energía.
• Movimiento circular y rotacional: Aceleración centrípeta, torque, momento de inercia y momento angular.
• Impulso y cantidad de movimiento: Conservación del momento lineal y colisiones.
• Oscilaciones y ondas: Movimiento armónico simple, características de ondas y fenómenos ondulatorios.
• Electromagnetismo: Campo eléctrico y magnético, fuerza magnética, leyes de Ampère y Faraday.
• Óptica: Reflexión, refracción, lentes y espejos.
• Fenómenos térmicos: Calor, temperatura, transferencia de energía y leyes de la termodinámica.

Estos temas son fundamentales no solo para aprobar el EXANI-II, sino también como base de estudios posteriores en áreas de ciencias e ingenierías.

---

SIMULADOR DE FÍSICA

Sistema de fuerza

1. Se improvisa el montaje de una rampa metálica para bajar cubos de cemento de 10 kg por acción de la fuerza de gravedad. Si la inclinación de dicha rampa es de 30°, ¿cuál es la fuerza de fricción que logra que los cubos se deslicen a una aceleración constante? Considere g=10 ms2 , sen 30° = 0.5, cos 30° = 0.87 y tan 30° =0.58.

1. 50 N
2. 87 N
3. 100 N

Resolución:

2. Una masa de 90 kg se desliza 30° hacia abajo sobre un plano inclinado. ¿Cuál es el valor necesario de la fuerza de fricción para que la masa se mueva a una velocidad constante? Considere g=10 m/s², sen 30° =0.5, cos 30° =0.87 y tan 30° =0.58.

1. 450 N
2. 783 N
3. 900 N

Resolución:

Respuesta correcta: a) 450 N

Para resolver este problema, necesitamos calcular la fuerza de fricción necesaria para que una masa de 90 kg se mueva hacia abajo sobre un plano inclinado con un ángulo de 30 grados respecto a la horizontal. Dado que queremos que la velocidad sea constante, la suma de las fuerzas en la dirección del movimiento debe ser igual a cero, según la segunda ley de Newton (∑F = 0).

Los datos proporcionados son:

• Masa (m) = 90 kg
• Aceleración debido a la gravedad (g) = 10 m/s²
• Ángulo de inclinación (θ) = 30 grados
• Seno de 30 grados (sen 30°) = 0.5

Primero, vamos a calcular la componente del peso de la masa en la dirección del movimiento. Para eso, usamos el seno del ángulo de inclinación:

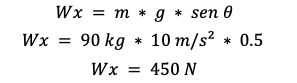
Ahora, sabemos que la fuerza de fricción debe ser igual en magnitud y en dirección opuesta a esta componente del peso para que la velocidad sea constante. Entonces, la fuerza de fricción (fr) es igual a 450 N, pero en dirección opuesta:

a) 450 N

Aceleración y fuerza centrípeta

3. Una persona y su moto, juntas, constituyen una masa de 300 kg. Si el conductor toma una curva con radio de 20 m a una velocidad de 10 m/s, ¿cuál es la fuerza centrípeta necesaria para que la moto consiga mantenerse en dicha curva?

1. 150 N
2. 300 N
3. 1 500 N
4. 3 000 N

Resolución:

Respuesta correcta: c) 1 500 N

Para calcular la fuerza centrípeta necesaria para que la moto mantenga su trayectoria en la curva, podemos utilizar la siguiente fórmula:

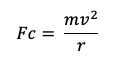
Los datos proporcionados son:

• Masa total (m) = 300 kg
• Velocidad lineal (v) = 10 m/s
• Radio de la curva (r) = 20 m

Ahora, sustituimos estos valores en la fórmula:

Entonces, la fuerza centrípeta necesaria para que la moto mantenga su trayectoria en la curva es de 1,500 N, como se mencionó en la opción C.

Trabajo y energía cinética rotacional

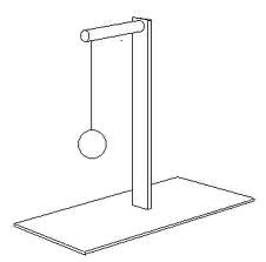
4. Para medir la velocidad del viento se construye un aparato de 3 copas, como el que se muestra en la imagen. Si cada copa tiene una masa de 0.2 kg y las varillas, de masa despreciable, tienen una longitud de 0.5 m, ¿cuál es el momento de inercia cuando el sistema rota?

1. 0.05 kg·m²
2. 0.10 kg·m²
3. 0.15 kg·m²

Resolución:

Respuesta correcta: c) 0.15 kg·m2

El momento de inercia (I) de un sistema de partículas se define como la suma de los productos de las masas de las partículas y el cuadrado de sus distancias al eje de rotación. Matemáticamente se expresa como:

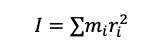
5. Se desea apretar una tuerca que se encuentra floja. Para que exista un torque máximo, la manera de agarrar la llave es…

1. lo más cerca posible de la cabeza de la llave
2. exactamente a la mitad de la llave
3. lo más alejado posible de la cabeza de la llave

Explicación:

Respuesta correcta: c) lo más alejado posible de la cabeza de la llave

El torque, también conocido como momento de fuerza, depende de dos factores principales: la magnitud de la fuerza aplicada y la distancia desde el punto de aplicación de la fuerza hasta el eje de rotación. Matemáticamente, el torque (τ) se calcula como el producto de la fuerza (F) aplicada y la longitud del brazo de palanca (r), es decir, τ = r × F. Aquí, r es la distancia perpendicular desde el eje de rotación hasta la línea de acción de la fuerza.

Para generar el máximo torque posible al apretar una tuerca con una llave, se debe aplicar la fuerza lo más alejado posible de la cabeza de la llave, que es donde se encuentra el eje de rotación de la tuerca. Al aumentar la distancia (r), se aumenta el torque para una misma cantidad de fuerza aplicada. Esto se debe al principio de palanca: cuanto más largo es el brazo de palanca, menos fuerza se necesita para generar un torque dado.

Por lo tanto, agarrar la llave lo más alejado posible de la cabeza de la llave aumenta la distancia r y, en consecuencia, maximiza el torque aplicado a la tuerca, lo que facilita su apriete. Las otras opciones, agarrar la llave más cerca de la cabeza o en la mitad, no proporcionan el máximo brazo de palanca posible y, por lo tanto, generan un torque menor para la misma fuerza aplicada.

Momento Angular

6. Un objeto colocado en la orilla de un disco tiene una cantidad de movimiento angular de 16 kg · m² s y gira a 20 · rad/s . Calcule el momento de inercia que presenta el objeto.

1. 0.04 kg · m²
2. 0.8 kg · m²
3. 1.25 kg · m²

Resolución:

Respuesta correcta: b) 0.8 kg·m2

Para resolver este problema, vamos a calcular el momento de inercia I de un objeto que gira. Utilizaremos la relación entre el momento angular L y el momento de inercia I, dada por la fórmula:

 7. Se tienen 2 masas unidas como se muestra en la figura. Si el sistema gira en torno al punto medio de la barra con una velocidad angular de 4 rads y la masa de la barra es despreciable, ¿cuál es el momento angular de las masas?

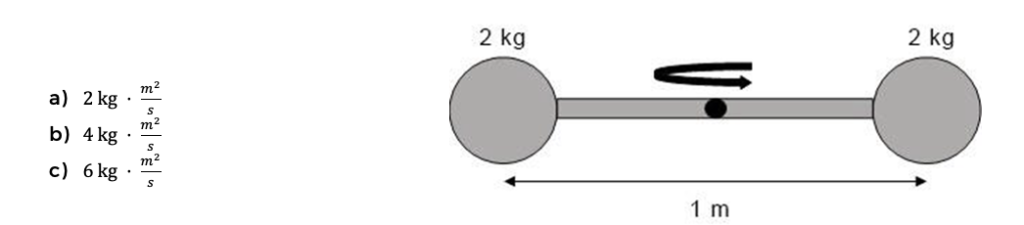
Resolución:

Respuesta correcta: b) 4 kg·m2s

El momento angular, L, es el producto del momento de inercia, I, y la velocidad angular, ω. El momento de inercia es una medida de la resistencia de un objeto a cambiar su estado de rotación y depende de la distribución de la masa del objeto y de la distancia de la masa al eje de rotación.

Para calcular el momento angular de este sistema, seguimos estos pasos:

Relación entre impulso y cantidad de movimiento

8. Un futbolista patea una pelota de 0.420 kg que se encuentra en reposo. La pelota avanza con una velocidad de 19 m/s. Considerando que el tiempo de contacto entre el pie y el balón dura 0.8 segundos, calcule la fuerza que se ejerce sobre el balón.

1. 6.384 N
2. 9.975 N
3. 56.548 N

Resolución:

Respuesta correcta: b) 9.975 N

Para calcular la fuerza ejercida sobre la pelota, utilizando la fórmula proporcionada, seguimos los siguientes pasos:

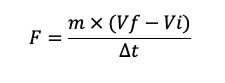
Donde:

• F es la fuerza.
• m es la masa de la pelota.
• Vf​ es la velocidad final.
• Vi​ es la velocidad inicial.
• Δt es el tiempo de contacto.

Sustituimos los valores conocidos:

• m= 0.420kg.
• Vf​= 19m/s (la velocidad final de la pelota).
• Vi​= 0m/s (la pelota estaba en reposo, por lo tanto, su velocidad inicial es 0).
• Δt= 0.8s.

Ahora, hacemos el cálculo:

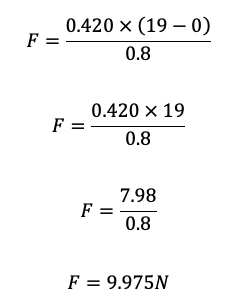
Por lo tanto, la fuerza ejercida sobre la pelota es aproximadamente 9.975N.

9. Sobre una superficie horizontal 2 esferas sólidas se deslizan sin fricción, de forma colineal. La primera se desplaza hacia la derecha a 10 m/s y su masa es de m₁ = 5 kg. La segunda se desplaza hacia la izquierda a 5 m/s y su masa es de m₂ = 5 kg. Si al colisionar ambas esferas se mantienen unidas, ¿cuál es la velocidad final después del choque? Considere el movimiento a la derecha como positivo y a la izquierda como negativo.

1. 2.5 m/s
2. 7.5 m/s
3. 15 m/s

Resolución:

Respuesta correcta: a) 2.5 m/s

Campos magnéticos y fuerza magnética

10. Calcule la magnitud de la inducción magnética B de una bobina helicoidal con 8 000 vueltas de 0.01 m de longitud y una corriente de 0.2 A. Considere π = 3 . 14 y µ₀ = 4 πx10^– 7 T ⋅ m / A .

1. 5x 10 – 4 T
2. 1x 10 – 1 T
3. 2x 10 – 1  T

Resolución:

Respuesta correcta: c) 2×10-1 T

11. Se coloca un imán dentro de una caja de cartón cuyas caras tienen un área de 0.01m² cada una. Si la densidad de flujo magnético es B = 2 x 10^-1 T, ¿qué cantidad de líneas de carga atraviesan la tapa?

1. 2 x 10^-3 Wb
2. 2 x 10¹ Wb
3. 5 x 10^-2 Wb

Resolución:

Respuesta correcta: a) 2 x 10-3 Wb

Para resolver este ejercicio, necesitamos entender la relación entre el flujo magnético (Φ), la densidad de flujo magnético (B), y el área a través de la cual el campo magnético pasa (A). La relación es dada por la ecuación del flujo magnético:

12. Determine la magnitud de la fuerza magnética sobre una partícula cargada con 4 µC y que se mueve a una velocidad perpendicular de 1500 m/s respecto al campo magnético de 0.12 T.

1. 4.8 x 10^-7 N
2. 7.2 x 10^-4 N
3. 7.2 x 10^-1 N

Resolución:

Respuesta correcta: b) 7.2 x 10-4 N

Para calcular la magnitud de la fuerza magnética que actúa sobre una partícula cargada que se mueve a través de un campo magnético, utilizamos la ley de Lorentz:

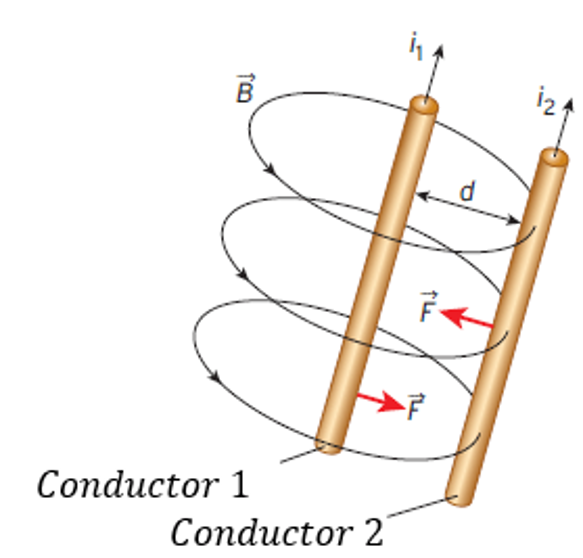
13. Calcule la distancia que separa a dos conductores rectos y paralelos que miden 0.5 m de largo, por cada uno de los cuales circula una corriente de 7 A en el mismo sentido y que resienten una fuerza de atracción de 2.25 x 10⁻⁴ N.

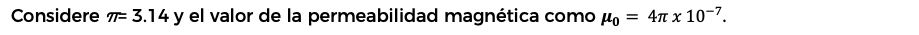
1. 0.003 m
2. 0.022 m
3. 0.087 m

Resolución:

Respuesta correcta: b) 0.022 m

Para resolver este problema, usaremos la ley de Ampère, que relaciona la fuerza entre dos conductores paralelos con la corriente que fluye a través de ellos y la distancia que los separa. La fórmula es la siguiente:

Aplicaciones del electromagnetismo

14. ¿Cuál dispositivo emplea ondas electromagnéticas para su funcionamiento?

1. Apuntador láser
2. Motor eléctrico
3. Bocina

Explicación:

Respuesta correcta: a) Apuntador láser

El dispositivo que emplea ondas electromagnéticas para su funcionamiento es el apuntador láser. Los apuntadores láser generan luz mediante la emisión estimulada de radiación, que es una forma de onda electromagnética. La luz láser es coherente y monocromática, lo que significa que tiene una fase constante en relación con el tiempo y espacio y una frecuencia muy precisa, respectivamente. Esto permite que los apuntadores láser sean muy precisos y se puedan utilizar para señalar con gran exactitud.

Por otro lado, los motores eléctricos y las bocinas no emplean ondas electromagnéticas en su funcionamiento principal:

• Un motor eléctrico convierte la energía eléctrica en energía mecánica mediante la interacción de campos magnéticos dentro del motor. No utiliza ondas electromagnéticas como las que se usan en la comunicación o en los láseres.
• Una bocina (altavoz) convierte las señales eléctricas en ondas sonoras mecánicas que podemos escuchar. Funciona mediante la vibración de una membrana que produce las ondas sonoras, que son fluctuaciones mecánicas en la presión del aire, y no ondas electromagnéticas.

Movimiento vibratorio armónico simple

15. ¿Cuál es la longitud de un péndulo que oscila con una frecuencia de 2.1 Hz? Considere π = 3.14 y g = 10 m/s².

1. 0.05 m
2. 0.12 m
3. 0.36 m

Resolución:

Respuesta correcta: a) 0.05 m

Para calcular la longitud (L) de un péndulo que oscila con una frecuencia de 2.1 Hz, podemos usar la fórmula para el período (T) de un péndulo simple:

Donde:

• T es el período del péndulo.
• L es la longitud del péndulo.
• g es la aceleración debida a la gravedad.

Dado que también sabemos que:

donde F es la frecuencia, podemos igualar estas dos expresiones para encontrar L:

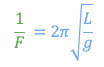
Ahora, despejamos L:

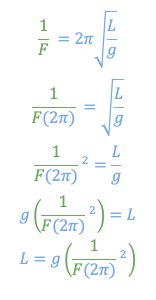
Dado que g = 10 m/s² y F = 2.1 Hz, sustituimos estos valores en la fórmula:

Por lo tanto, la longitud del péndulo es aproximadamente 0.05 metros, como se mencionó en la opción A.

16. Seleccione el ejemplo en el que se describe un movimiento armónico simple.

1. El aleteo de un ave al emprender el vuelo
2. La cuerda de una guitarra al ser rasgada
3. Los pasos al descender de una pendiente

Explicación:

Respuesta correcta: b) La cuerda de una guitarra al ser rasgada

El ejemplo que describe un movimiento armónico simple (MAS) es “La cuerda de una guitarra al ser rasgada”. El MAS es un tipo de movimiento periódico o vibratorio que se caracteriza por ser regular y repetitivo, y por ocurrir en un medio elástico. En el caso de la cuerda de una guitarra, cuando se rasga, esta vibra alrededor de su posición de equilibrio y lo hace de manera periódica, con una amplitud, frecuencia y periodo bien definidos. Esta vibración corresponde a un movimiento armónico simple ya que la fuerza restauradora (que lleva a la cuerda de vuelta a su posición original) es proporcional a la desviación de la cuerda de su posición de reposo.

En cuanto a las otras opciones:

• “El aleteo de un ave al emprender el vuelo” no es un movimiento armónico simple. Aunque el movimiento de las alas puede ser periódico, no es armónico porque no se caracteriza por una fuerza restauradora proporcional a la desviación desde una posición de equilibrio, y porque involucra una serie de complejidades dinámicas que difieren del MAS.
• “Los pasos al descender de una pendiente” tampoco son un ejemplo de movimiento armónico simple. Aunque el movimiento de caminar implica cierta periodicidad, no cumple con las características del MAS, como la existencia de una fuerza restauradora proporcional a la desviación desde un punto de equilibrio.

Ondas y fenómenos ondulatorios

17. Las partículas de una onda mecánica transversal vibran _______ a la dirección de la propagación.

1. Paralelamente
2. Perpendicularmente
3. Oblicuamente

Explicación:

Respuesta correcta: b) Perpendicularmente

En el contexto de las ondas mecánicas transversales, la opción correcta es “perpendicularmente”. Esto se debe a que, por definición, en una onda transversal, las partículas del medio por el que se propaga la onda se mueven de manera perpendicular a la dirección de propagación de la onda. Es decir, si la onda se mueve horizontalmente, las partículas se desplazarán verticalmente hacia arriba y hacia abajo.

Las otras opciones no son correctas por las siguientes razones:

• “Paralelamente” describe el comportamiento de las ondas longitudinales, no de las transversales. En una onda longitudinal, las partículas se mueven en la misma dirección en que se propaga la onda, como sucede en el sonido que se propaga en el aire.
• “Oblicuamente” implica un movimiento en un ángulo que no es ni paralelo ni perpendicular a la dirección de propagación de la onda. Este tipo de movimiento no caracteriza a las ondas transversales ni a las longitudinales, por lo que no es aplicable en este contexto.

18. Identifique en la imagen el número que corresponde al nodo.

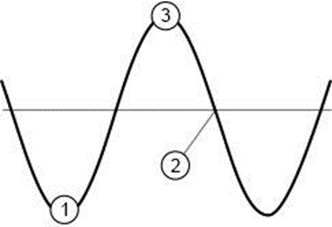
1. 1
2. 2
3. 3

Explicación:

Respuesta correcta: 2

La imagen muestra una onda representada gráficamente con tres puntos marcados: 1, 2 y 3. En una onda, el nodo es el punto donde la onda cruza la línea de equilibrio, es decir, donde no hay desplazamiento vertical desde la posición de equilibrio.

En la imagen, el punto marcado con el número 2 se encuentra en la línea de equilibrio de la onda, y no muestra desplazamiento vertical desde esa línea, lo cual lo identifica como un nodo.

Los puntos marcados con los números 1 y 3 no son nodos: el punto 1 está en el valle, el punto más bajo de la onda, y el punto 3 está en la cresta, el punto más alto de la onda. Estos son los puntos de máxima amplitud de la onda y están en las posiciones opuestas a un nodo. Por lo tanto, la respuesta correcta es el punto 2, ya que es el que representa un nodo.

Ondas electromagnéticas

19. Calcule la longitud de la onda electromagnética que se propaga a partir de una antena que emite una frecuencia de 6 000 Hz. Considere c = 3 x 10⁸ m/s.

1. 2×10^-5m
2. 5×10⁴m
3. 2×10⁴m

Resolución:

Respuesta correcta: b) 5×10⁴m

Para calcular la longitud de onda (λ) de una onda electromagnética con una frecuencia de 6,000 Hz, puedes usar la ecuación:

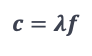
Donde:

• c es la velocidad de la luz, que es igual a 3×10⁸ m/s.
• λ es la longitud de onda que queremos encontrar.
• f es la frecuencia, que es igual a 6,000Hz.

Ahora, despejamos λ:

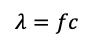
Sustituyendo los valores dados:

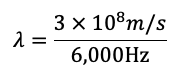
Para el EXANI-II, donde solo se permite el uso de calculadoras básicas, es necesario convertir los exponentes en números decimales para realizar las operaciones. Esto se hace moviendo el punto decimal en el número según el exponente, en este caso mover el punto 8 veces (agregar 8 ceros al 3) dando como resultado: 300,000,000.

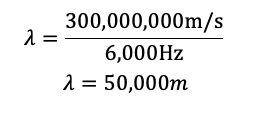
Entonces, la longitud de onda de la onda electromagnética es de 5×10⁴metros, como se menciona en las opción B.

Óptica geométrica y ondulatoria

20. Se coloca un objeto a 4 cm de una lente divergente cuya distancia focal es de 20 cm.

Calcule la distancia a la que se formará la imagen.

1. -5 cm
2. -3.33 cm
3. -0.3 cm

Resolución:

Respuesta correcta: b) -3.33 cm

Para resolver este ejercicio vamos a utilizar la fórmula de la distancia focal de una lente y la fórmula de la distancia de la imagen para una lente divergente. Aquí están las fórmulas que vamos a usar:

Fórmula de la distancia focal de una lente:

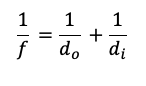
Donde:

• f es la distancia focal de la lente (en este caso, 20 cm, pero recuerda que la distancia focal de una lente divergente es negativa).
• d_o​ es la distancia del objeto a la lente (en este caso, 4 cm).
• d_i​ es la distancia de la imagen a la lente (lo que estamos tratando de calcular).

Primero debemos convertir la distancia focal de la lente en notación negativa, ya que es una lente divergente. La distancia focal f es -20 cm. Ahora podemos sustituir los valores conocidos en la fórmula de la distancia focal de la lente:

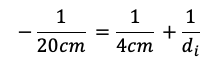
Ahora despejamos d_i​ 

Restamos los valores:

21. Determine el índice de refracción de una sustancia cuando la velocidad de la luz en ella es de 2.56 x 10⁸ m/s. Considere la velocidad de la luz en el vacío c = 3 x 10⁸ m/s.

1. 0.85
2. 1.17
3. 7.68

Resolución:

Respuesta correcta: b) 1.17

El índice de refracción, n, de una sustancia se puede calcular usando la relación entre la velocidad de la luz en el vacío, c, y la velocidad de la luz en la sustancia, v, mediante la fórmula:

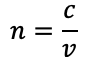
Donde:

• n es el índice de refracción,
• c es la velocidad de la luz en el vacío,
• v es la velocidad de la luz en la sustancia.

Sustituyamos los valores dados:

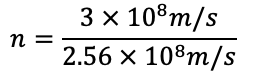
Podemos simplificar la notacion cientifica porque al tener ambos el mismo exponente multiplicando a su numero podemos eliminarlos:

El resultado se redondea generalmente a dos cifras decimales (a menos que se especifique otra cosa), por lo tanto:

n≈1.17

La opción correcta es la b) 1.17.

22. Las lentes divergentes generan imágenes de…

1. menor tamaño, virtuales y no invertidas
2. mayor tamaño, reales e invertidas
3. igual tamaño, reales e invertidas

Explicación:

Respuesta correcta: a) menor tamaño, virtuales y no invertidas

Las lentes divergentes son conocidas por dispersar los rayos de luz que pasan a través de ellas. Esto significa que los rayos de luz parecen originarse de un punto focal detrás de la lente. Debido a esta dispersión de los rayos, las lentes divergentes no pueden formar imágenes reales en las que los rayos de luz realmente convergen; en su lugar, forman imágenes virtuales que parecen estar detrás de la lente.

La imagen que se forma a través de una lente divergente es siempre virtual, lo que significa que no puede proyectarse sobre una pantalla, porque los rayos de luz no se encuentran realmente en la posición de la imagen. Además, es una imagen derecha, es decir, no invertida, porque la lente divergente no invierte las partes superior e inferior de la imagen como lo haría una lente convergente. Finalmente, la imagen es más pequeña que el objeto, porque los rayos de luz se alejan entre sí, lo que hace que la imagen parezca más pequeña de lo que es el objeto en realidad.

En contraste, las lentes convergentes pueden formar imágenes reales e invertidas cuando el objeto se coloca más allá del punto focal de la lente. Dependiendo de la posición del objeto con respecto al punto focal y al centro óptico de la lente convergente, la imagen puede ser mayor o menor en tamaño. Por ejemplo, si un objeto está colocado en el doble de la distancia focal de una lente convergente, la imagen formada es real, invertida y del mismo tamaño que el objeto. Esto es diferente de las propiedades de las imágenes formadas por lentes divergentes.

Reflexión y refracción

23. Al observar un haz de luz que penetra un lago en total calma, pareciera como si el haz se doblara al entrar al agua, desviándose con un cierto ángulo de su trayectoria original. ¿Qué característica define a este fenómeno de la luz?

1. Refracción
2. Difracción
3. Reflexión

Explicación:

Respuesta correcta: a) Refracción

El fenómeno descrito, donde un haz de luz se dobla o cambia de dirección al pasar de un medio a otro de diferente densidad óptica, como del aire al agua, se conoce como refracción. La refracción ocurre debido al cambio en la velocidad de la luz al pasar de un medio a otro. La luz viaja a diferentes velocidades en diferentes medios, y cuando pasa de un medio menos denso (como el aire) a un medio más denso (como el agua), disminuye su velocidad y cambia de dirección. Este cambio de dirección es el que hace que el haz de luz parezca doblarse en la interfaz entre los dos medios.

Las otras opciones, difracción y reflexión, no describen correctamente el fenómeno observado:

• La difracción se refiere a la capacidad de la luz para doblarse alrededor de los bordes de un obstáculo o a través de una abertura, lo cual no es el caso en el escenario descrito.
• La reflexión se refiere al cambio de dirección de la luz al rebotar en una superficie, no al cambiar de un medio a otro, por lo que tampoco aplica en este contexto.

---

Recomendaciones finales

Para aprovechar este simulador al máximo:

• Entrena con límite de tiempo: El examen real tiene presión, acostúmbrate a trabajar bajo esas condiciones.
• Analiza cada error: No te conformes con la respuesta correcta; entiende el porqué de cada resultado.
• Domina las bases: Refuerza cinemática, leyes de Newton y energía, ya que son ejes recurrentes en muchos problemas.
• Haz simulacros completos: No te limites a resolver ejercicios sueltos; entrena tu resistencia mental y concentración.
• Apóyate en explicaciones extendidas: En Pasatuexam tendrás acceso a material premium con guías paso a paso, ejemplos resueltos y técnicas rápidas para responder reactivos.

Empieza gratis con las preguntas liberadas en este simulador, y cuando quieras llevar tu preparación al siguiente nivel, desbloquea el curso completo de Pasatuexam. Así tendrás un plan estructurado, más reactivos, y la seguridad de que estás cubriendo absolutamente todo lo necesario para quedarte en la universidad de tus sueños.