Derivadas por definición, de funciones trigonométricas, de funciones exponenciales y logarítmicas y de funciones polinomiales
- Derivadas por definición, de funciones trigonométricas, de funciones exponenciales y logarítmicas y de funciones polinomiales
- Derivada por definición
- Interpretación Geométrica
- Derivadas de funciones trigonométricas
- Derivadas de funciones exponenciales y logarítmicas
- Derivadas de funciones polinomiales
- Formulario de Calculo Diferencial (más importantes para el EXANI-II)
- Formulario de Derivadas (Otras formulas)
- Ejercicios EXANI-II
- 🚀 ¡Potencia tu Preparación con Nuestro Plan Profesional! 🎓
Derivada por definición
La derivada de una función f(x) en un punto x0 se define como el límite de la tasa de cambio promedio de la función en un intervalo que tiende a cero. Matemáticamente, se expresa como:

Donde f´(x₀) es la derivada de f(x) en el punto x₀.
Aplicación Correcta
- Expresión Correcta: En la fórmula, es esencial que tanto f(x) como f(x₀) estén completamente desarrolladas y encerradas en paréntesis para mantener la estructura de la resta entre ambas expresiones.
- Orden de Resta: La estructura de la fórmula debe ser f(x)-f(x₀). Si se invierte el orden (haciendo f(x₀)-f(x)), el resultado sería la negación de la derivada, es decir, -f´(x₀).
- Uso de Límites: El cálculo de la derivada implica la evaluación de un límite. Esto significa que el valor de x se acerca a x₀de tal manera que el denominador x-x₀ no sea cero, pero la distancia entre x y x₀ sea tan pequeña como sea posible.
Ejemplos
Supongamos que tenemos una función cuadrática f(x)=ax²+bx+c. La derivada de esta función en un punto x₀ se calcularía aplicando la definición:

Siguiendo esta estructura, se garantiza que se está aplicando correctamente la definición de la derivada.
Ejemplo de Gráficas de Funciones Simples:
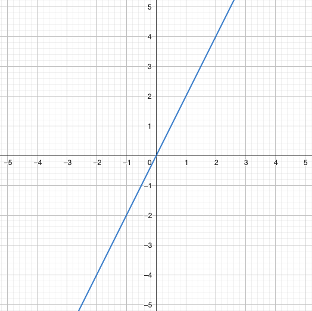
Función Lineal (f(x)=3x)
Para f(x)=3x, la derivada en cualquier punto es f´(x)= 3. Esto significa que la función aumenta constantemente a una tasa de 3 unidades en y por cada unidad en x que avanza.
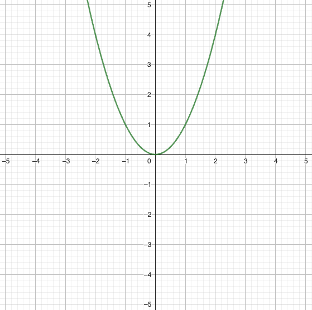
Función Cuadrática (g(x)=x²)
Tomemos g(x)=x². Aquí, la derivada cambia con x, específicamente, g´(x)=2x². Esto indica que la tasa de cambio de g(x) se incrementa a medida que x se hace más grande. Por ejemplo, en x=1, g´(1)=2, lo que significa que la pendiente de la tangente (y, por lo tanto, la tasa de cambio) en ese punto es 2.
En resumen, la derivada en un punto puede compararse con la lectura de un velocímetro en un automóvil en un momento específico, indicando la velocidad instantánea en ese instante. Al igual que un velocímetro muestra la rapidez exacta del auto en cada segundo, la derivada muestra la rapidez de cambio de la función en cada punto. Geométricamente, es como observar la inclinación de la carretera en un punto dado: una pendiente ascendente (derivada positiva) indica que el auto sube, una descendente (derivada negativa) que baja, y una pendiente plana (derivada cero) sugiere que el auto se desplaza en un tramo recto y nivelado. Esta analogía ayuda a visualizar cómo una función se incrementa, disminuye o se mantiene constante en diferentes puntos.
Importante:

En cálculo, la notación d/dx es una forma convencional de representar la operación de derivación. El símbolo “d” proviene de la palabra “diferencial”, y x es la variable independiente con respecto a la cual se está tomando la derivada. Cuando colocamos d/dx antes de una función, estamos indicando que queremos calcular la tasa de cambio instantánea de esa función en relación con la variable .
Por ejemplo, si tenemos una función y=f(x), la expresión:

representa la derivada de f respecto a x, es decir, la rapidez con la que f(x) cambia a medida que x cambia.
Esta notación fue introducida en el siglo XVII por el matemático Gottfried Wilhelm Leibniz, y es una de las dos notaciones principales para derivadas, siendo la otra la notación de “prima” (por ejemplo, f´(x)), utilizada por Isaac Newton. La notación de Leibniz es particularmente útil cuando queremos ser explícitos acerca de la variable de diferenciación, lo que la hace muy práctica en casos donde hay múltiples variables en juego o cuando se realizan operaciones más complejas como derivadas parciales, integrales, y en la definición de la derivada misma.
Interpretación Geométrica
Pendiente de la Tangente:
En un gráfico, la derivada en un punto específico de una función corresponde a la pendiente de la línea tangente a la curva en ese punto. La línea tangente es aquella que roza la curva en ese punto y solo en ese punto, sin cortarla ni desviarse de ella. Por ejemplo: Si la curva de una función es una carretera, la derivada en un punto sería la inclinación de esa carretera en ese punto exacto. Una derivada positiva indica una subida, una negativa una bajada, y una derivada cero un tramo plano.
Análisis de Comportamiento:
Crecimiento y Decrecimiento: Una función está creciendo en los puntos donde su derivada es positiva y decreciendo donde la derivada es negativa. Esto es similar a saber si un vehículo está acelerando (derivada positiva) o desacelerando (derivada negativa).
Puntos Críticos y Extremos: Los puntos donde la derivada es cero son de especial interés. Estos puntos, conocidos como puntos críticos, pueden ser máximos o mínimos locales de la función. En términos prácticos, son como los puntos más altos o más bajos en una montaña rusa.
Ejemplo Práctico:
Movimiento de un Objeto (Física): En física, si una función describe la posición de un objeto en el tiempo, la derivada de esa función en un tiempo dado nos da la velocidad del objeto en ese momento. La derivada de la velocidad (es decir, la segunda derivada de la posición) nos da la aceleración.
Derivadas de funciones trigonométricas
Las funciones trigonométricas son fundamentales en matemáticas, especialmente en cálculo, física e ingeniería. La comprensión de sus derivadas es crucial para analizar fenómenos periódicos como ondas y movimientos circulares. Aquí detallamos las derivadas de las funciones trigonométricas básicas y algunas de sus aplicaciones.
Funciones Básicas y sus Derivadas (Las más importantes para el EXANI-II):
- Seno (sin(x)):
- Derivada: La derivada de sin(x) es cos(x). En física, se usa para modelar fenómenos oscilatorios, como el movimiento de un péndulo.
- Coseno (cos(x)):
- Derivada: La derivada de cos(x) es -sin(x). Utilizada en análisis de ondas y para describir el movimiento armónico simple.
- Tangente (tan(x)):
- Derivada: La derivada de tan (x) es sec²(x). Puede ser aplicada en problemas de optimización y en geometría analítica.
Derivadas de Funciones Trigonométricas Inversas:
- Arcoseno (Arc sin(x)):
- Derivada:

Utilizada en cálculos de trayectorias y en mecánica.
- Arcocoseno (Arc cos(x)):
- Derivada:

Importante en el cálculo de ángulos y en la trigonometría esférica.
- Arcotangente (Arc tan(x)):
- Derivada:

Se usa en la integración y en el análisis de funciones racionales.
Derivadas de Funciones Trigonométricas Hiperbólicas:
- Seno Hiperbólico (sin h(x)):
- Derivada: cos h(x).
Aparece en el estudio de curvas catenarias y en la teoría de la relatividad.
- Derivada: cos h(x).
- Coseno Hiperbólico (cos h(x)):
- Derivada: sin h(x).
Utilizado en cálculos de distribuciones de tensión y en geometría hiperbólica.
- Derivada: sin h(x).
- Tangente Hiperbólica (tan h(x)):
- Derivada: tan h(x).
Empleada en estadística y en el análisis de ciertos tipos de ecuaciones diferenciales.
- Derivada: tan h(x).
Derivadas de funciones exponenciales y logarítmicas
Las funciones exponenciales y logarítmicas desempeñan un papel central en diversas áreas del cálculo, la física, la biología y la economía, entre otras disciplinas. Comprender sus derivadas es crucial para modelar el crecimiento, el decaimiento y otros procesos dinámicos.
Funciones Exponenciales y sus Derivadas
- Función Exponencial Natural aˣ:
- Derivada: (eˣ)´=eˣ. Se utiliza para modelar el crecimiento y decaimiento exponencial, como en poblaciones o en desintegración radiactiva.
- Función Exponencial con Base General
:
- Derivada: (aˣ)´=aˣIn(a), donde a>0 y a≠1. Usada en finanzas para modelar el crecimiento de inversiones y en biología para el crecimiento de poblaciones.
Las funciones exponenciales son las únicas funciones que son iguales a sus propias derivadas, lo que las hace indispensables en la solución de ecuaciones diferenciales.
Funciones Logarítmicas y sus Derivadas:
- Logaritmo Natural In(x):
- Derivada: (In(x))´= 1/x para x>0. Utilizado en análisis de tasas de cambio relativas, como en la ley de enfriamiento de Newton.
- Logaritmo en Base General Logₐ(x):
- Derivada: (Logₐ(x))´ para x>0 y a>0. Importante en teoría de la información y en la modelación de escalas logarítmicas.
La interacción entre las funciones exponenciales y logarítmicas es intrigante debido a su naturaleza inversa. Esto implica que sus derivadas están intrínsecamente relacionadas. El estudio de estas derivadas no solo es un ejercicio en matemáticas puras, sino también una exploración de cómo las funciones crecen y decrecen a ritmos variables y cómo se puede cuantificar este cambio de manera matemática rigurosa.
La constante e juega un rol crucial en estas derivaciones debido a sus propiedades únicas relacionadas con las tasas de cambio. La comprensión de eˣ y In(x) es esencial para entender las derivadas en este contexto, ya que sus comportamientos y propiedades son centrales en el cálculo diferencial.
Derivadas de funciones polinomiales
Un polinomio es una expresión matemática que consiste en términos que son sumas o diferencias de productos de números (coeficientes) y variables elevadas a potencias enteras no negativas. La forma general de un polinomio de grado n es:

Donde:

La derivada de una función polinomial se obtiene aplicando las reglas básicas de derivación a cada término del polinomio. La derivación es una operación lineal, lo que significa que la derivada de una suma (o resta) de funciones es la suma (o resta) de sus derivadas.
Regla del Poder (Potencia)
La regla del poder es fundamental para derivar polinomios. Esta regla establece que si tienes una función f(x)=xⁿ, donde es un número entero, entonces la derivada de f con respecto a x es:

Esta regla se aplica término a término en el polinomio.
Ejemplo EXANI-II

Para derivar un polinomio, aplicamos la regla del poder a cada término por separado, consideremos el polinomio
Para encontrar la derivada Q′(x), aplicamos la regla del poder a cada término:
- Derivada de 6x⁵:
- Aplicamos nxⁿ⁻¹ con n=5.
- Resultado: 30x⁴.
- Derivada de -4x⁴:
- Aplicamos nxⁿ⁻¹ con n=4.
- Resultado: -16x³.
- Derivada de 3x³:
- Aplicamos nxⁿ⁻¹ con n=3.
- Resultado: 9x²
- Derivada de -2x²:
- Aplicamos nxⁿ⁻¹con n=2.
- Resultado: -4x.
- Derivada de x:
- La derivada de x (que es x¹) es simplemente su coeficiente, 1.
- Derivada de la constante
:
- La derivada de cualquier constante es 0.
Sumando todas estas derivadas obtenemos:

Otros ejemplos en el plan profesional…
Recuerda siempre que:
- Términos Constantes: Cualquier término constante en un polinomio (es decir, un término sin x) se vuelve 0 al derivar.
- Coeficientes: Los coeficientes se mantienen multiplicando la derivada del término correspondiente.
- Grado del Polinomio Derivado: La derivada de un polinomio de grado
es un polinomio de grado n-1.
Regla del Producto
La regla del producto es un método fundamental en la derivación que se utiliza cuando se tiene una función que es el producto de dos funciones distintas. Esta regla es crucial para calcular la derivada de productos de funciones.
Fórmula de la Regla del Producto
Si tenemos dos funciones diferenciables, digamos f(x) y g(x), entonces la derivada de su producto f(x)g(x) se da por la siguiente fórmula:

Donde:
- f´(x) y g´(x) son las derivadas de f(x) y g(x), respectivamente.
Aplicación de la Regla del Producto
- Derivar la Primera Función f(x):
- Calcula la derivada de f(x).
- Denota esta derivada como f´(x).
- Multiplicar esta Derivada por la Segunda Función g(x):
- Multiplica f´(x) por g(x).
- Denota este producto como Parte1(P1)=f´(x)*g(x)
- Derivar la Segunda Función g(x):
- Calcula la derivada de g(x).
- Denota esta derivada como g´(x).
- Multiplicar esta Derivada por la Primera Función g(x):
- Multiplica g´(x) por f(x).
- Denota este producto como parte2(P2)=g´(x)*f(x).
- Sumar los Dos Productos Resultantes:
- Suma P1 y P2.
- La suma de estos productos es la derivada del producto de las funciones:

Ejemplo EXANI-II
Para aplicar la regla del producto a las funciones f(x)=2x³-x y g(x)=x²+3 y encontrar la derivada del producto R(x)=f(x)g(x), seguimos los siguientes pasos:
- Derivar f(x):
- La función f(x)=2x³-x se deriva como f´(x)=6x²-1.
- Derivar g(x):
- La función g(x)=x²+3 se deriva como g´(x)=2x.
- Aplicar la Regla del Producto:
- Multiplicamos f´(x) por g(x) y f(x) por g´(x), y luego sumamos los resultados.
- Esto nos da: (6x²-1)(x²+3)+(2x³-x)(2x)
- Multiplicar para obtener el Primer Producto (6x²-1)(x²+3):
- Multiplicamos 6x² por cada término en x²+3:
6x²*x²+6x²*3
6x⁴+18x² - Multiplicamos -1 por cada termino en x²+3:
-1*x²-1*3
-x²-3 - Al combinarlos nos da 6x⁴+18x²-x²-3
- Multiplicamos 6x² por cada término en x²+3:
- Multiplicar para obtener el Segundo Producto (2x³-x)(2x):
- Multiplicamos 2x³ por 2x
2x³*2x
4x⁴ - Multiplicacomos -x por 2x
-x*2x
-2x² - Al combinar nos da 4x⁴-2x²
- Multiplicamos 2x³ por 2x
- Combinar los Resultados:
- Sumanos los tétminos de ambos productos
(6x⁴+18x²-x²-3)+(4x⁴-2x²) - Al combinar términos semejantes, obtenemos:
6x⁴+18x²-x²-3+4x⁴-2x²
6x⁴+4x⁴+18x²-x²-2x²-3
10x⁴+15x²-3
- Sumanos los tétminos de ambos productos
Por lo tanto, la expresión simplificada es:

Regla del Cociente
La regla del cociente se aplica cuando se tiene una función que es el cociente de dos funciones. Esta regla es esencial para derivar tales cocientes.
Fórmula de la Regla del Cociente
Para dos funciones diferenciables, f(X) y g(x), con g(x) no siendo cero, la derivada del cociente g(x)f(x) es:

O resumiendo la regla:

Aplicación de la Regla del Cociente
Para aplicar la regla del cociente a cualquier par de funciones f(x) y g(x) y encontrar la derivada de su cociente, puedes seguir estos pasos. Este procedimiento general te ayudará a calcular la derivada de un cociente de funciones:
- Derivar la Función del Numerador f(x):
- Calcula la derivada de f(x).
- Denota esta derivada como f´(x).
- Multiplicar esta Derivada por la Función del Denominador g(x):
- Multiplica f´(x) por g(x).
- Denota este producto como Parte1(P1)=f´(x)*g(x).
- Derivar la Función del Denominador g(x):
- Calcula la derivada de g(x).
- Denota esta derivada como g´(x).
- Multiplicar esta Derivada por la Función del Numerador f(x):
- Multiplica g´(x) por f(x).
- Denota este producto como Parte2(P2)=g´(x)*f(x).
- Restar el Segundo Producto del Primero:
- Resta P2 de P1.
- El resultado es la diferencia entre los dos productos: D=P1-P2.
- Esta diferencia es D=f´(x)*g(x)-g´(x)*f(x).
- Dividir el Resultado por el Cuadrado de la Función del Denominador [k(x)]²:
- Calcula el cuadrado de g(x), denotado como [g(x)]².
- Divide D por [g(x)]².
- El resultado final es la derivada del cociente de las funciones:

Este procedimiento te permitirá aplicar la regla del cociente para calcular la derivada de un cociente de dos funciones f(x) y g(x), independientemente de las funciones específicas involucradas.
Ejemplo de Aplicación
Para aplicar la regla del cociente a las funciones (2x+5)/x² y encontrar la derivada aplicamos la regla del cociente, entonces seguiremos los siguientes pasos:
1. Derivar la Función del Numerador f(x):
Función del numerador:
- Tenemos f(x)=2x+5.
Proceso de derivación:
- La derivada de un término axⁿ respecto a x es anxⁿ⁻¹.
- Aplicamos esto al primer término 2x, que es de la forma axⁿ donde a=2 y n=1.
- La derivada de 2x con respecto a x es 2*1*x¹⁻¹, lo cual simplifica a 2.
- El segundo término, 5, es una constante, y la derivada de una constante es 0.
Resultado de la derivada:
- Entonces, la derivada del numerador es f´(x)=2.
2. Multiplicar esta Derivada por la Función del Denominador g(x):
Función del denominador:
- Tenemos g(x)=x².
Producto de la derivada del numerador por el denominador:
- Multiplicamos la derivada del numerador, f´(x)=2, por el denominador g(x)=x².
- El producto es P1=2*x².
3. Derivar la Función del Denominador g(x):
Proceso de derivación:
- Aplicamos la regla de la potencia anxⁿ⁻¹ al término x², donde a=1 y n=2.
- La derivada de x² con respecto a x es 2*x²⁻¹, lo cual simplifica a
.
Resultado de la derivada:
- Por lo tanto, la derivada del denominador es g´(x)=2x.
4. Multiplicar esta Derivada por la Función del Numerador f(x):
Producto de la derivada del denominador por el numerador:
- Multiplicamos la derivada del denominador, g´(x)=2x, por el numerador f(x)=2x+5.
- El producto es P2=2x*(2x+5).
5. Restar el Segundo Producto del Primero:
Diferencia de los productos:
- Restamos el producto P2 del productoP1: P1-P2.
- Esto se expande a 2x²-(2x*(2x+5)).
6. Dividir el Resultado por el Cuadrado de la Función del Denominador (g(x))²:
Cuadrado de la función del denominador:
- Calculamos (x²)², que es x⁴.
División del resultado por el cuadrado del denominador:
- Dividimos la diferencia P1-P2 por x⁴.
- Esto nos da la derivada del cociente, que es:

7. Simplificar el Resultado:
Simplificación:
- Expandimos y simplificamos el numerador 2x²-2x*(2x+5).
- Esto da 2x²-4x²-10
- Simplificando, obtenemos -2x²-10x.
- Dividimos esto por x⁴ para obtener la derivada simplificada.
Entonces la derivada simplificada del cociente es:

Regla de la Cadena
La regla de la cadena es una técnica fundamental en el cálculo diferencial utilizada para encontrar la derivada de una función compuesta. Una función compuesta se forma cuando una función se aplica dentro de otra, como h(x)=f(g(x)). La regla de la cadena nos permite calcular la derivada de en términos de las derivadas de f y g.
Fórmula de la Regla de la Cadena
Si tenemos dos funciones diferenciables f(u) y g(x), y si h(x)=f(g(x)), entonces la derivada de h con respecto a x se da por:

Donde:
- f´(u) es la derivada de f con respecto a u.
- g´(x) es la derivada de g con respecto a x.
Aplicación de la Regla de la Cadena Generalizada
La regla de la cadena es un método fundamental en cálculo diferencial para encontrar la derivada de funciones compuestas. Aquí se describe una guía generalizada en cuatro pasos para aplicar esta regla en cualquier problema similar:
Paso 1: Identificar las Funciones Interna y Externa
- Función Interna: Identifica la parte de la función compuesta que se encuentra “dentro” de otra función. Esta es tu función interna, denotada como g(x).
- Función Externa: Identifica la función que actúa sobre la función interna. Esta es tu función externa, denotada como f(u), donde u es el resultado de la función interna g(x).
Paso 2: Derivar la Función Externa
- Deriva f(u) con respecto a u: Calcula la derivada de la función externa como si u fuera la variable independiente. La derivada resultante es f´(u).
Paso 3: Derivar la Función Interna
- Deriva g(x) con respecto a x: Calcula la derivada de la función interna con respecto a la variable independiente original x. La derivada resultante es g´(x).
Paso 4: Multiplicar las Derivadas
- Multiplica y Combina las Derivadas: Multiplica la derivada de la función externa evaluada en la función interna, f´(g(x)), por la derivada de la función interna, g´(x). El resultado es la derivada de la función compuesta h(x).
Ejemplo de Aplicación
Consideremos una función compuesta h(x)=(3x²+2)⁴. Aquí, g(x)=3x²+2 y f(u)=u⁴.
Paso 1: Identificar las Funciones Interna y Externa
- Función Interna g(x):
- En nuestro ejemplo, la función interna es la expresión dentro del paréntesis: g(x)=3x²+2.
- Esta función se “introduce” en otra función, que en este caso es la función de elevar a la cuarta potencia.
- Función Externa f(u):
- La función externa actúa sobre la función interna. En este caso, es la operación de elevar al cuadrado, pero aplicada a la función interna. Si u=g(x), entonces la función externa es f(u)=u⁴.
Paso 2: Derivar las Funciones Individualmente
- Derivar la Función Interna g(x):
- Tomamos la derivada de g(x=3x²+2) con respecto a x, lo que nos da g´(x)=6x.
- Derivar la Función Externa f(u):
- La derivada de f(u)=u⁴ respecto a u es f´(u)=4u³.
Paso 3: Aplicar la Regla de la Cadena

- Multiplicar las Derivadas:
- La regla de la cadena nos dice que debemos multiplicar la derivada de la función externa evaluada en la función interna, f´(g(x)), por la derivada de la función interna, g´(x).
- Esto significa que reemplazamos u en f´(u)=4u³ por g(x)=3x²+2, obteniendo 4(3x²+2)³.
- Luego, multiplicamos este resultado por g´(x)=6x.
- Al sustituir todos nuestros datos en la formula obtenemos:

Paso 4: Simplificar la Expresión
- Simplificación:
- Finalmente, multiplicamos los términos para simplificar la expresión.
- Esto nos da h´(x)=24x(3x²+2)³ como resultado final.
Formulario de Calculo Diferencial (más importantes para el EXANI-II)

Formulario de Derivadas (Otras formulas)

Ejercicios EXANI-II
Ejemplo 1 (Ejercicio tomado del simulador EXANI-II):
Seleccione el límite de la función f(x)=9x²+12x+3, por medio del cual se obtiene la derivada por definición.

Resolución:
Para encontrar la derivada de una función por definición, utilizamos el límite de la diferencia de la función evaluada en x y en x₀, dividida por x-x₀, cuando x tiende a x₀. La fórmula general de la derivada por definición es:

Para la función f(x)=9x²+12x+3, la derivada por definición sería:

Vamos a ver por qué la segunda opción es la correcta:

La correcta aplicación de estos pasos nos da la expresión del segundo inciso:

Este límite, cuando se calcula, nos dará la derivada de la función f(x) en el punto x₀, y es el procedimiento correcto según la definición de la derivada por límites.
Ejemplo 2 (Ejercicio tomado del simulador EXANI-II):
Calcule la derivada de la función polinomial: f(x)=x³+4x²+2x-7
- 3x²+8x
- 3x²+8x+2
- 3x²+4+2
Resolución:
La imagen muestra un ejercicio matemático sobre la derivación de una función polinómica. La función es f(x)x³+x²+2x-7, y se presentan tres opciones de derivadas, con explicaciones sobre por qué son correctas o incorrectas.
Para calcular la derivada de f(x), aplicaremos la regla de la potencia que dice que la derivada de xn es nxⁿ⁻¹, donde n es un número real. Además, la derivada de una constante es cero y la derivada de una suma (o resta) de términos es la suma (o resta) de sus derivadas individuales. Sigamos estos pasos:
- Derivar x³: Aplicando la regla de la potencia, la derivada es x³⁻¹, que simplifica a 3x².
- Derivar 4x²: De nuevo, aplicamos la regla de la potencia y obtenemos 2*4x²⁻¹, que se simplifica a 8x.
- Derivar 2x: La derivada de x es 1, y al multiplicar por la constante 2, se mantiene igual, entonces la derivada de 2x es 2.
- Derivar -7: La derivada de una constante es cero, por lo tanto, la derivada de −7 es 0.
Sumando todas estas derivadas individuales, obtenemos la derivada de la función completa:

La opción correcta es “3x²+8x+2”, que corresponde a la segunda opción mostrada en la imagen. Las otras opciones son incorrectas por asumir que no se deriva la constante en el caso de la primera opción, y por mantener la constante -7 en la derivada en el caso de la tercera opción.
Ejemplo 3 (Ejercicio tomado del simulador EXANI-II):
¿Cuál es la derivada del cociente siguiente?

Resolución:
Para aplicar la regla del cociente a las funciones y encontrar la derivada aplicamos la regla del cociente, entonces seguiremos los siguientes pasos:
1. Derivar la Función del Numerador f(x):
Función del numerador:
- Tenemos f(x)=2x+5.
Proceso de derivación:
- La derivada de un término axⁿ respecto a x es anxⁿ⁻¹.
- Aplicamos esto al primer término 2x, que es de la forma axⁿ donde a=2 y n=1.
- La derivada de 2x con respecto a x es 2*1*x¹⁻¹, lo cual simplifica a 2.
- El segundo término, 5, es una constante, y la derivada de una constante es 0.
Resultado de la derivada:
- Entonces, la derivada del numerador es f´(x)=2.
2. Multiplicar esta Derivada por la Función del Denominador g(x):
Función del denominador:
- Tenemos g(x)=x².
Producto de la derivada del numerador por el denominador:
- Multiplicamos la derivada del numerador, f´(x)=2, por el denominador g(x)=x².
- El producto es P1=2*x².
3. Derivar la Función del Denominador g(x):
Proceso de derivación:
- Aplicamos la regla de la potencia anxⁿ⁻¹ al término x², donde a=1 y n=2.
- La derivada de x² con respecto a x es 2*x²⁻¹, lo cual simplifica a 2x.
Resultado de la derivada:
- Por lo tanto, la derivada del denominador es g´(x)=2x.
4. Multiplicar esta Derivada por la Función del Numerador f(x):
Producto de la derivada del denominador por el numerador:
- Multiplicamos la derivada del denominador, g´(x)=2x, por el numerador f(x)=2x+5.
- El producto es P2=2x*(2x+5).
5. Restar el Segundo Producto del Primero:
Diferencia de los productos:
- Restamos el producto P2 del producto P1: P1-P2.
- Esto se expande a 2x²-(2x*(2x+5)).
6. Dividir el Resultado por el Cuadrado de la Función del Denominador (g(x))²:
Cuadrado de la función del denominador:
- Calculamos (x²)², que es x⁴.
División del resultado por el cuadrado del denominador:
- Dividimos la diferencia P1-P2 por x⁴.
- Esto nos da la derivada del cociente, que es:

7. Simplificar el Resultado:
Simplificación:
- Expandimos y simplificamos el numerador 2x²-2x*(2x+5).
- Esto da 2x²-4x²-10x
- Simplificando, obtenemos -2x²-10x.
- Dividimos esto por
para obtener la derivada simplificada.
Entonces la derivada simplificada del cociente es:

🚀 ¡Potencia tu Preparación con Nuestro Plan Profesional! 🎓
Si has empezado a descubrir cómo prepararte para el EXANI-II con nuestro contenido gratuito, ¡te felicitamos! 🌟 Pero, ¿estás listo para dar el gran salto? Con nuestro Plan Profesional, no solo vas un paso adelante, ¡vas a volar! 🚀
Al elegir el Plan Profesional, desbloquearás acceso a:
- Contenido sin Publicidad y sin Interrupciones 🚫: Estudia con la máxima concentración, sin anuncios que te distraigan de tus objetivos.
- Contenido de Calidad 100% Basado en las Guías del EXANI-II 📚: Confía en un material que sigue fielmente el currículo oficial, maximizando tu eficacia en el estudio.
- Lecciones Escritas y Videos Explicativos 📝🎥: Visualiza conceptos complejos con materiales diseñados para facilitar tu aprendizaje.
- Explicaciones Paso a Paso 📘: Todo se entiende mejor con nuestros métodos sencillos y claros.
- Preguntas Como en el Examen ❓: Practica con ejercicios que te preparan de verdad, aumentando tu seguridad al máximo.
- Simuladores de Examen 💻: Siente el día del examen antes de llegar, para que nada te sorprenda.
- Acceso Multiplataforma 📱💻: Aprende cuando quieras y desde cualquier dispositivo, facilitando tu preparación en todo momento.
Asegura tu acceso al éxito con el Plan Profesional. No es solo preparación, es tu boleto para lograr tus sueños universitarios. ¡Decídete ya! 🌈 No dejes pasar esta oportunidad. ⏳ ¡El tiempo vuela y tu futuro te espera!
🌟 Simulador Gratis 🌟
Si estás curioso sobre lo que el Plan Profesional puede ofrecerte, te tenemos una sorpresa. Haz clic aquí y enfrenta nuestro simulador especial. Con solo 30 preguntas, podrás medir qué tan preparado estás para tu examen de admisión. 🎯
Esta es tu oportunidad de obtener un vistazo de la calidad y profundidad que nuestro Plan Profesional tiene para ofrecer, y al mismo tiempo, evaluar tu nivel actual de preparación. 💪
