Medidas de Tendencia central y de Dispersión (Media aritmética y Desviación Estándar) para el EXANI-II

La estadística es una herramienta esencial en la comprensión y análisis de datos en diversos campos. Entre sus conceptos más importantes se encuentran las medidas de tendencia central y de dispersión. La media aritmética, una medida de tendencia central, es el promedio de un conjunto de números y se utiliza ampliamente para representar el valor “típico” de un conjunto de datos. Por otro lado, la desviación estándar, una medida de dispersión, indica cuánto se alejan los valores individuales en un conjunto de datos del valor medio. Este concepto es crucial para entender cuán dispersos o concentrados están los datos alrededor de la media.

Dominar estos temas es fundamental para tener un buen desempeño en las preguntas de estadística del EXANI-II. Asegúrate de comprender bien estos conceptos y practicarlos con ejemplos y ejercicios, ya que esto te preparará de manera efectiva para las preguntas en el EXANI-II.

Medidas de Tendencia Central (Media aritmética)

Las medidas de tendencia central son estadísticas que nos ayudan a determinar el valor representativo de un conjunto de datos. Estas medidas nos indican dónde se encuentra el “centro” de la distribución de datos, es decir, dónde se agrupan la mayoría de los valores. Las tres medidas más comunes de tendencia central son:

Media Aritmética

La media aritmética es el valor promedio de un conjunto de datos. Se calcula sumando todos los valores y dividiendo el resultado entre el número de datos.

Fórmula:

Ejemplo: Si tenemos un conjunto de calificaciones en una clase: [85, 92, 78, 88, 95], la media aritmética sería:

Mediana

La mediana es el valor que se encuentra justo en el medio de un conjunto de datos cuando se ordena de manera ascendente. Divide el conjunto de datos en dos partes iguales.

Para encontrar la mediana, primero ordena los datos y luego selecciona el valor del medio.

• Ejemplo: Si tenemos un conjunto de edades: [25, 18, 32, 40, 28], primero ordenamos los datos: [18, 25, 28, 32, 40], y la mediana es 28, ya que es el valor del medio.

Moda

La moda es el valor que aparece con mayor frecuencia en un conjunto de datos. Puede haber una moda (unimodal), dos modas (bimodal) o más (multimodal) en un conjunto de datos.

• Ejemplo 1 (unimodal): Si tenemos un conjunto de colores de camisetas: [“rojo”, “azul”, “verde”, “rojo”, “amarillo”], la moda es “rojo” ya que aparece dos veces, más que cualquier otro color.
• Ejemplo 2 (bimodal): Si tenemos un conjunto de números de lotería ganadores: [5, 12, 17, 5, 22, 17], la moda es “5” y “17”, ya que ambos aparecen dos veces, más que cualquier otro número.

Medidas de Dispersión (Varianza y Desviación Estándar)

Las medidas de dispersión cuantifican la variabilidad o la extensión de un conjunto de datos. Mientras que las medidas de tendencia central nos dicen dónde se concentran los datos, las medidas de dispersión nos indican cuán dispersos o dispersas están las observaciones en relación con la medida central. Aquí, exploraremos cuatro medidas de dispersión comunes:

Rango

El rango es la diferencia entre el valor máximo y el valor mínimo en un conjunto de datos. Es la medida más simple de dispersión.

Fórmula del Rango:

Rango = Valor Máximo − Valor Mínimo

Ejemplo: Consideremos el conjunto de datos: [12, 18, 24, 30, 36].

• Valor Mínimo = 12
• Valor Máximo = 36
• Resolución: Rango = 36 – 12 = 24

Desviación Media

La desviación media mide cuánto se desvían los datos de la media aritmética. Se calcula tomando la diferencia entre cada valor y la media, tomando el valor absoluto de esa diferencia y luego promediando esas diferencias absolutas.

Fórmula de la Desviación Media:

Ejemplo: Consideremos el conjunto de datos: [14, 18, 22, 26, 30].

Resolución:

Primero calculamos la media:

Con la media calculada podemos comenzar a calcular la desviación media:

Varianza

La varianza mide cuánto se dispersan los datos con respecto a la media. Se calcula tomando la diferencia entre cada valor y la media, elevando al cuadrado esa diferencia y luego promediando los cuadrados de las diferencias.

Fórmula de la Varianza para población:

Fórmula de la Varianza para muestra:

Ejemplo: Consideremos el conjunto de datos: [10, 12, 14, 16, 18].

Resolución:

Primero calculamos la media:

Con la media calculada podemos comenzar a calcular la desviación media:

Desviación Estándar

La desviación estándar es simplemente la raíz cuadrada de la varianza. Proporciona una medida de dispersión en la misma unidad que los datos originales.

Fórmula de la Desviación Estándar:

Ejemplo: Utilizaremos la varianza calculada previamente: Varianza = 8.

Resolución:

Interpretación de Medidas Descriptivas

Las medidas descriptivas en estadística son herramientas cruciales para resumir y entender las características de un conjunto de datos. Estas medidas incluyen las de tendencia central y dispersión, cada una aportando diferentes perspectivas sobre los datos. La correcta interpretación de estas medidas es esencial para analizar datos de manera efectiva en EXANI-II.

Interpretación de la Media Aritmética

La media aritmética, o promedio, ofrece una visión general de dónde se sitúan los valores de un conjunto de datos. Una media alta sugiere que la mayoría de los valores son relativamente altos, mientras que una media baja indica lo contrario. Sin embargo, es importante recordar que la media puede verse afectada por valores extremos (outliers). Por tanto, si hay valores extremadamente altos o bajos, la media podría no representar adecuadamente la “típica” experiencia de todos los datos.

Interpretación de la Mediana

La mediana, el valor medio en un conjunto de datos ordenados, es menos sensible a los valores extremos en comparación con la media. Si la mediana es significativamente diferente de la media, esto podría indicar una distribución asimétrica de los datos. Por ejemplo, una mediana mucho más baja que la media sugiere una distribución sesgada hacia la derecha.

Interpretación de la Moda

La moda, el valor más frecuente en un conjunto de datos, es útil para identificar el valor más común. En datos con distribuciones multimodales, es decir, con varias modas, esto puede indicar la presencia de diferentes grupos o categorías dentro del conjunto de datos.

Interpretación de la Varianza y Desviación Estándar

La varianza y la desviación estándar son medidas de dispersión que indican cuán dispersos están los datos respecto a la media. Una varianza o desviación estándar alta significa que los datos están muy dispersos, es decir, hay una gran variabilidad en los datos. Por otro lado, una varianza o desviación estándar baja indica que los datos están más agrupados alrededor de la media. Estas medidas son particularmente útiles para comparar la dispersión en diferentes conjuntos de datos.

Interpretación del Rango

El rango, que es la diferencia entre el valor máximo y mínimo, proporciona una idea rápida de la extensión de los datos. Un rango amplio sugiere una gran diferencia entre los valores más altos y más bajos, mientras que un rango estrecho indica que los datos están más concentrados.

Vídeo Resumen

Preguntas EXANI-II

Pregunta 1 (Ejercicio tomado del Simulador EXANI-II):

En la gráfica se muestra el número de pares de zapatos vendidos en una tienda por día hábil.

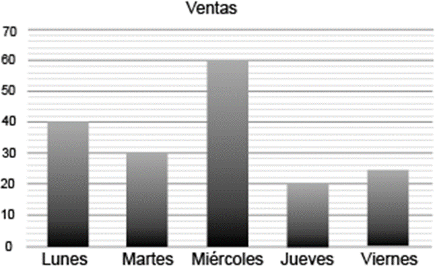
¿Cuál es la media aritmética del número de pares vendidos durante esos días?

a) 30
b) 35
c) 60

Explicación

Respuesta correcta: b) 35. La media aritmética se calcula sumando el número de pares de zapatos vendidos cada día y dividiendo entre el número de días. La suma de las ventas diarias es 40 + 30 + 60 + 20 + 25 = 175. Al dividir 175 entre 5 días, obtenemos una media de 35 pares de zapatos vendidos por día.

---

Pregunta 2 (Ejercicio tomado del Simulador EXANI-II):

¿Qué conjunto de números presenta una desviación estándar mayor?        

a) {13, 10, 24, 8, 15, 20}
b) {16, 16, 9, 12, 12, 16}
c) {19, 14, 17, 15, 18, 16}

Explicación

Respuesta correcta: a) {13, 10, 24, 8, 15, 20}. La desviación estándar es una medida de cuánto se dispersan los datos respecto a su media. El conjunto a) tiene valores que varían más ampliamente y están más alejados entre sí en comparación con los otros conjuntos, lo que indica una mayor dispersión alrededor de la media, que es 15.

---

Pregunta 3 (Ejercicio tomado del Simulador EXANI-II):

Una escuela organiza una selección de futbol. Para elegir a la última integrante se considera el número de goles de 2 estudiantes, en los 5 últimos partidos.

María		Julia
Número de partido	Número de goles anotados	Número de partido	Número de goles anotados
1	2	1	4
2	4	2	4
3	4	3	3
4	4	4	4
5	6	5	5

De acuerdo con la tabla, se observa que ambas tienen un promedio de 4 goles, pero el entrenador quiere que su desempeño en el partido no se aleje mucho de dicho promedio. Para elegir a la última integrante del equipo, el entrenador debe considerar a…

a. María, ya que sus datos tienen el doble de dispersión que los de Julia, por lo que tiene el doble de rendimiento
b. Julia, ya que la dispersión de su número de goles es menor que la de María
c. Otras candidatas, ya que la dispersión de los datos de María y Julia es menor que su media

Explicación

Respuesta correcta: b) Julia, ya que la dispersión de su número de goles es menor que la de María. La desviación estándar es menor para Julia, lo que indica que sus goles están más concentrados alrededor del promedio de 4 goles. Por tanto, es más consistente en su rendimiento según la preferencia del entrenador de que el desempeño no se aleje mucho del promedio.

---

🚀 ¡Potencia tu Preparación con Nuestro Plan Profesional! 🎓

Si has empezado a descubrir cómo prepararte para el EXANI-II con nuestro contenido gratuito, ¡te felicitamos! 🌟 Pero, ¿estás listo para dar el gran salto? Con nuestro Plan Profesional, no solo vas un paso adelante, ¡vas a volar! 🚀

vAl elegir el Plan Profesional, desbloquearás acceso a:

• Contenido sin Publicidad y sin Interrupciones 🚫: Estudia con la máxima concentración, sin anuncios que te distraigan de tus objetivos.
• Contenido de Calidad 100% Basado en las Guías del EXANI-II 📚: Confía en un material que sigue fielmente el currículo oficial, maximizando tu eficacia en el estudio.
• Lecciones Escritas y Videos Explicativos 📝🎥: Visualiza conceptos complejos con materiales diseñados para facilitar tu aprendizaje.

• Explicaciones Paso a Paso 📘: Todo se entiende mejor con nuestros métodos sencillos y claros.
• Preguntas Como en el Examen ❓: Practica con ejercicios que te preparan de verdad, aumentando tu seguridad al máximo.
• Simuladores de Examen 💻: Siente el día del examen antes de llegar, para que nada te sorprenda.
• Acceso Multiplataforma 📱💻: Aprende cuando quieras y desde cualquier dispositivo, facilitando tu preparación en todo momento.

Asegura tu acceso al éxito con el Plan Profesional. No es solo preparación, es tu boleto para lograr tus sueños universitarios. ¡Decídete ya! 🌈  No dejes pasar esta oportunidad. ⏳ ¡El tiempo vuela y tu futuro te espera!

🌟 Simulador Gratis 🌟

Si estás curioso sobre lo que el Plan Profesional puede ofrecerte, te tenemos una sorpresa. Haz clic aquí y enfrenta nuestro simulador especial. Con solo 30 preguntas, podrás medir qué tan preparado estás para tu examen de admisión. 🎯

Esta es tu oportunidad de obtener un vistazo de la calidad y profundidad que nuestro Plan Profesional tiene para ofrecer, y al mismo tiempo, evaluar tu nivel actual de preparación. 💪