El módulo de Aritmética en el EXANI-II evalúa tu capacidad para resolver operaciones y problemas básicos con números reales, fracciones, decimales y proporciones. Aunque muchos piensan que son temas “fáciles”, la realidad es que la presión del examen y la precisión que se requiere pueden hacer la diferencia entre un buen y un mal puntaje.
Este simulador gratuito te permitirá practicar con preguntas similares a las del examen real, divididas por tema para que sepas exactamente en qué área necesitas reforzar. Algunos temas estarán disponibles gratis, mientras que otros requieren el acceso completo al curso de Pasatuexam, donde encontrarás explicaciones extendidas, ejemplos resueltos paso a paso y técnicas para resolver más rápido.
¿Qué mide este simulador de Aritmética?
El simulador busca evaluar tu dominio de los principios fundamentales de los números reales y las operaciones básicas. Entre los temas que abarca están:
- Principios de números reales: leyes de los signos, exponentes y jerarquía de operaciones.
- Símbolos de agrupación: paréntesis, corchetes y llaves.
- Múltiplos y divisores: MCD, MCM y factorización.
- Números racionales: razones, proporciones, variaciones y problemas cotidianos.
- Aplicaciones prácticas: porcentajes, descuentos, reglas de tres, escalas y problemas de producción o consumo.
Estos temas son clave porque se repiten en gran parte de los módulos de ciencias exactas y son base para avanzar en problemas de álgebra, cálculo o física.
SIMULADOR DE ARITMÉTICA
Principios de números reales: Leyes de los signos
1. Identifique la expresión matemática que utilice correctamente los símbolos de agrupación.
- 3 – (7 + [4(5 – 9) – 3(-5)])
- 3 – {7 + [4(5 – 9) – 3(-5)}
- 3 – {7[4(5 – 9) – 3(-5)]}
Resolución
Respuesta correcta: a) 3 – (7 + [4(5 – 9) – 3(-5)])
Para identificar la expresión matemática que utiliza correctamente los símbolos de agrupación, es importante verificar que cada tipo de símbolo de agrupación (paréntesis, corchetes, llaves) esté correctamente emparejado y en el orden adecuado. Los paréntesis se utilizan para las operaciones más internas, seguidos por los corchetes para operaciones intermedias, y las llaves para las más externas. Vamos a analizar cada una de las expresiones dadas:
a) 3 – (7 + [4(5 – 9) – 3(-5)])
- Paréntesis: (5 – 9) y (-5) están correctamente emparejados.
- Corchetes: [4(5 – 9) – 3(-5)] también están correctamente > emparejados.
- No hay llaves en esta expresión.
Esta expresión utiliza correctamente los paréntesis y corchetes, pero no incluye llaves.
b) 3 – {7 + [4(5 – 9) – 3(-5)}
- Paréntesis: (5 – 9) y (-5) están correctamente emparejados.
- Corchetes: [4(5 – 9) – 3(-5)] están correctamente emparejados.
- Llaves: {7 + [4(5 – 9) – 3(-5)} aquí hay un problema, ya que la > llave de apertura { no tiene su correspondiente llave de > cierre }.
Esta expresión no utiliza correctamente los símbolos de agrupación debido a las llaves desemparejadas.
c) 3 – {7[4(5 – 9) – 3(-5)]}
- Paréntesis: (5 – 9) y (-5) están correctamente emparejados.
- Corchetes: [4(5 – 9) – 3(-5)] también están correctamente > emparejados.
- Llaves: {7[4(5 – 9) – 3(-5)]} están correctamente emparejadas.
Esta expresión utiliza paréntesis para las operaciones más internas, corchetes para las intermedias, y llaves para la operación más externa. Dado que la tercera opción cumple con el uso correcto de los tres tipos de símbolos de agrupación (paréntesis, corchetes y llaves), y cada uno de ellos está correctamente emparejado y ordenado de acuerdo con su jerarquía, podemos concluir que la opción 3 es la expresión matemática que utiliza correctamente los símbolos de agrupación.
2. Identifique la situación en la que se aplica la ley de los signos que corresponde al producto de un número negativo por uno positivo.
- Una persona tiene un capital invertido de $5,000 en un negocio y a los 2 meses pierde $1,200
- La temperatura de una ciudad es de 6 °C bajo cero y durante la madrugada desciende el doble
- Un empleado tiene una deuda de $7,500 y en 3 meses la incrementa $3,000
Resolución
Respuesta correcta: b) La temperatura de una ciudad es de 6 °C bajo cero y durante la madrugada desciende el doble
La ley de los signos para el producto indica que cuando multiplicamos un número negativo por uno positivo, el resultado es negativo. Vamos a analizar cada situación para ver cuál se ajusta a esta regla:
a) Una persona tiene un capital invertido de $5,000 en un negocio y a los 2 meses pierde $1,200
- Aquí, la pérdida de $1,200 podría interpretarse como un número negativo (-$1,200), pero no hay un número positivo con el que se esté multiplicando directamente en esta situación. La inversión inicial de $5,000 es positiva, pero no hay una multiplicación explícita entre estos dos valores en el contexto de la pérdida.
b) La temperatura de una ciudad es de 6 °C bajo cero y durante la madrugada desciende el doble
- En este caso, la temperatura inicial de -6 °C (un número negativo) se multiplica por 2 (un número positivo). Al multiplicar -6 °C por 2, el resultado es -12 °C, lo cual es coherente con la ley de los signos para el producto de un número negativo y un número positivo.
c) Un empleado tiene una deuda de $7,500 y en 3 meses la incrementa $3,000
- Similar al primer caso, la deuda inicial puede considerarse un número negativo (-$7,500), pero el incremento de la deuda en $3,000 no implica una multiplicación entre un número negativo y un número positivo. Más bien, es una adición de dos cantidades negativas.
Por lo tanto, la situación que mejor representa la aplicación de la ley de los signos en el producto de un número negativo por uno positivo es la opción b) La temperatura de una ciudad es de 6 °C bajo cero y durante la madrugada desciende el doble.
Principios de números reales: Leyes de los exponentes
3. Si la velocidad de un meteorito es de 6×10⁷m/s, la distancia entre dos planetas es de 6.432×10¹³m y la fórmula del tiempo es distancia sobre velocidad, identifique, en segundos, el tiempo que le toma al meteorito viajar de un planeta a otro.
- 1.072×10⁻⁶
- 1.072×10⁶
- 1.072×10²⁰
Resolución
Respuesta correcta: b) 1.072×10⁶
Para calcular el tiempo que le toma al meteorito viajar de un planeta a otro, se usa la fórmula del tiempo t=vd, donde d es la distancia y v es la velocidad. Vamos a hacer este cálculo:

4. Identifique la representación en lenguaje común correspondiente a la siguiente expresión matemática.
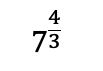
- Raíz cuarta de siete elevado al cubo
- Tercera parte de siete elevado a la cuarta potencia
- Raíz cúbica de siete elevado a la cuarta potencia
Resolución
Respuesta correcta: c) Raíz cúbica de siete elevado a la cuarta potencia

Raíz cúbica de siete elevado a la cuarta potencia.
5. Identifique la expresión aritmética que corresponde al siguiente planteamiento. La cuarta potencia de cinco octavos elevado a la tres.
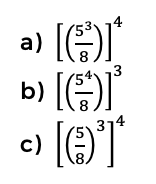

Principios de números reales: Jerarquía de operaciones
6. Identifique la solución de la siguiente expresión.
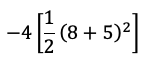
- -338
- -324
- -66
Resolución
Respuesta correcta: a) -338
Para resolver la expresión matemática dada, seguiremos la jerarquía de las operaciones: primero paréntesis, luego exponenciación, después multiplicación y división, y finalmente suma y resta. La expresión es:
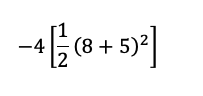
Sigamos paso a paso:

7. Un trabajador aprovecha sus días vacacionales para ir de paseo en coche.
El lunes recorrió 80 km, el martes avanzó de la distancia recorrida el lunes y el miércoles manejó
de la distancia recorrida el martes, pero de vuelta a su casa.
¿A cuántos kilómetros, expresados en fracción, quedó el trabajador del punto de partida?
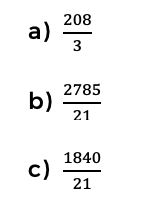
Resolución

8. En un almacén de frijol, al principio del periodo se contaba con 5 000 kg de producto. Primeramente, se realizaron 5 ventas de 333.333 kg cada una, luego 8 ventas de 240.45 kg cada una y, por último, se hicieron 3 compras de 725.32 kg cada una. ¿Cuántos kilogramos quedaron en el almacén al final del periodo, considerando el resultado redondeado a dos decimales?
- 3 585.70
- 5 151.54
- 6 414.31
Resolución

9. Identifique la solución de la siguiente expresión.
72 ÷ 8 + 3 – 4 × 5 + 4 × 2² ÷ 2 – 6
- -6
- -1
- 82
Resolución
Respuesta correcta: a) -6
Para resolver la expresión matemática, seguimos la jerarquía de operaciones: primero realizamos las operaciones de exponentes, luego multiplicaciones y divisiones de izquierda a derecha y, finalmente, sumas y restas de izquierda a derecha. La expresión es:

Principios de números reales: Múltiplos y divisores
10. Un apicultor que produce miel y propóleo desea envasar la totalidad de su producción en recipientes iguales de la máxima capacidad posible. En sus últimas cosechas obtuvo 256 y 96 L, respectivamente. ¿Cuál tiene que ser la capacidad de los recipientes, expresada en litros?
- 16
- 32
- 48
Resolución
Respuesta correcta: b) 32
Para encontrar la capacidad de los recipientes de manera que se puedan envasar completamente tanto la miel como el propóleo sin que sobre nada, necesitamos calcular el máximo común divisor (MCD) de las cantidades de miel y propóleo. El MCD es el mayor número que divide a ambos números sin dejar residuo.
Los números que tenemos son 256 L de miel y 96 L de propóleo. Veamos cómo calcular el MCD de 256 y 96 paso a paso:

Por lo tanto, el MCD de 256 y 96 es 32 L, que es la mayor capacidad posible para los recipientes que permitirá envasar toda la producción de miel y propóleo sin que sobre nada.
11. La torre de control de un aeródromo registra 3 vuelos diarios. Uno cada 8, otro cada 12 y uno más cada 15 horas. Si los 3 vuelos coinciden en un momento, ¿después de cuántas horas será la próxima vez que coincidan nuevamente?
- 60
- 120
- 240
Resolución
Respuesta correcta: b) 120
Para determinar cuándo los tres vuelos coincidirán nuevamente, se debe encontrar el mínimo común múltiplo (MCM) de los intervalos de tiempo entre los vuelos. El MCM es el número más pequeño que es múltiplo de todos ellos.
Los intervalos de tiempo son de 8, 12 y 15 horas. Calcularemos el MCM de estos tres números:

12. Identifique la solución de la siguiente operación.
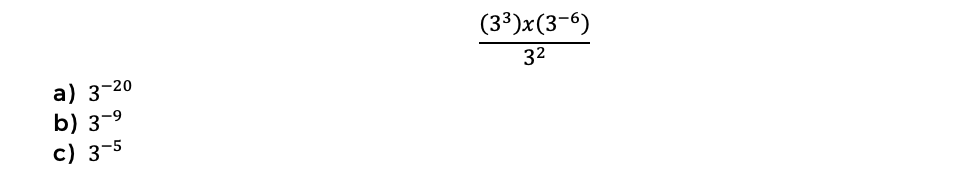
Resolución
Respuesta correcta: c) 3⁻⁵
Para resolver la operación con exponentes, utilizamos las propiedades de las potencias. La operación es:

13. Identifique los factores primos del número 350.
- 2, 3, 7
- 2, 5, 7
- 5, 7, 13
Resolución
Respuesta correcta: b) 2, 5, 7
Para encontrar los factores primos del número 350, debemos descomponerlo en sus factores primos básicos. La descomposición en factores primos consiste en dividir el número entre los primos más pequeños posibles hasta que el cociente sea 1.
Comenzamos con el número 350:

Problemas con números racionales: Razones
14. En una comunidad de 20 personas, de las cuales 8 son menores, se tiene previsto que diariamente un adulto haga guardia nocturna para permitir el acceso a la comunidad. Se requiere un cronograma para que se turnen de manera equitativa de las 21:00 a las 06:00 horas del día siguiente. ¿Cuántas horas hace de guardia cada adulto durante 360 días?
- 162
- 270
- 405
Resolución
Respuesta correcta: b) 270
Para calcular cuántas horas hace de guardia cada adulto durante 360 días, seguimos estos pasos:

15. Un aparato de sonido en casa requiere 24 V para alimentarse. Se sabe que 2 baterías de 3 V conectadas en serie proporción un voltaje de 6 V. Si se desea hacer funcionar el aparato utilizando baterías, ¿Cuántas se necesitan?
- 4
- 8
- 12
Resolución
Respuesta correcta: b) 8
Si cada par de baterías de 3 V conectadas en serie proporciona un voltaje de 6 V, entonces, para obtener 24 V, necesitamos hacer la siguiente operación:

16. Diariamente, una fábrica produce 5 000 pantalones con 10 máquinas en un tiempo de 5 horas. Si se sabe que 2 máquinas estarán en mantenimiento y no podrán operar, **¿Cuántas horas se incrementará el tiempo de producción diario?
- 1.25
- 4.00
- 6.25
Resolución
Respuesta correcta: a) 1.25
La producción de pantalones en esta fábrica sigue una relación de proporcionalidad inversa entre el número de máquinas y el tiempo necesario para producir una cantidad fija de pantalones. Esto significa que si disminuye el número de máquinas, el tiempo de producción aumentará, y viceversa.
La relación se puede expresar con la fórmula:

17. Identifique la gráfica que representa el rendimiento de combustible, equivalente a 10 km/L, de una camioneta.
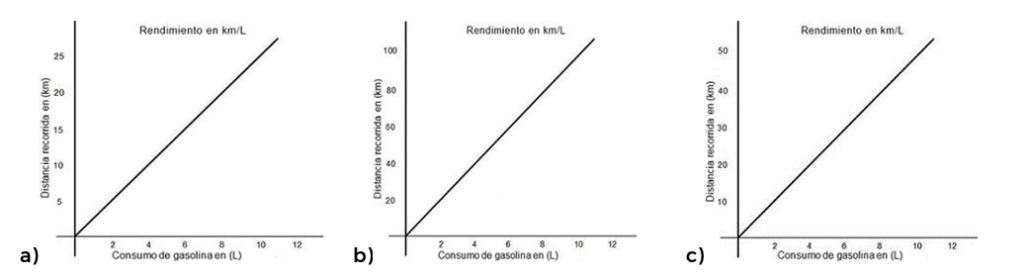
Resolución
Respuesta correcta: opcion c
Para identificar la gráfica correcta que representa el rendimiento de combustible equivalente a 10 km/L, buscaremos la línea que muestra una proporción directa entre la distancia recorrida y el consumo de gasolina. Un rendimiento de 10 km/L significa que por cada litro de gasolina, la camioneta puede recorrer 10 kilómetros.
La gráfica que representa correctamente el rendimiento de combustible de una camioneta que tiene un rendimiento de 10 km/L sería aquella en la cual por cada litro de combustible (en el eje de las abscisas), la camioneta pueda recorrer 10 km (en el eje de las ordenadas). Es decir, si en el eje horizontal (Consumo de gasolina en L) se marca 1, entonces en el eje vertical (Distancia recorrida en km) debería marcar 10, y así sucesivamente manteniendo la misma proporción.
La segunda imagen muestra esa relación directa y proporcional: por cada litro de combustible, la camioneta recorre 10 km. Por ejemplo, a los 2 litros corresponde a 20 km, a los 3 litros a 30 km y así sucesivamente, lo cual es consistente con un rendimiento de 10 km/L. Por lo tanto, la tercera imagen es la que representa correctamente el rendimiento de la camioneta.
18. Una empresa tiene 5 departamentos, cada uno de ellos con diferente número de extensiones telefónicas. El Almacén cuenta con 4 extensiones; Mantenimiento, con 3; Producción, con 4; Control de Calidad, con 7, y Ventas, con 3. La empresa dicta que el pago del servicio telefónico se realiza en forma proporcional al número de extensiones de cada departamento. Para este mes, el recibo asciende a $28,412.00. ¿Cuánto debe pagar el Departamento de Ventas por el servicio?
- $4,058.86
- $5,682.40
- $9,470.67
Respuesta correcta: a) $4,058.86
Para calcular cuánto debe pagar el Departamento de Ventas por el servicio telefónico, sigamos el proceso:

19. Con 18% de descuento aplicado, un traje cuesta $2,050. ¿Cuál es su precio original?
- $1,681
- $2,419
- $2,500
Resolución
Respuesta correcta: c) $2,500

20. La tripulación de un barco está conformada por 70 personas. Se cuenta con alimento para 18 días con 3 comidas diarias. Si se disminuyen las raciones a 2 comidas diarias y se aumenta la tripulación con 15 personas, ¿Cuántos días durarán los alimentos?
- 21.85
- 22.23
- 32.78
Resolución
Respuesta correcta: b) 22.23
Para resolver este problema, primero calculamos la cantidad total de comidas que se pueden servir con la provisión de alimentos, y luego determinamos cuántos días durarán estas comidas con la nueva cantidad de personas y raciones diarias.
- Calculamos el total de comidas con la tripulación original:
- La tripulación original es de 70 personas.
- Tienen alimentos para 18 días.
- Se sirven 3 comidas al día.
Multiplicamos el número de personas por el número de comidas por día y luego por el número de días para obtener el total de comidas:

21. La capacidad de una cisterna es de 6 045 L. Si se llena con agua de un grifo a razón de 65 L cada 3 minutos, ¿Cuántos minutos tardará en llenarse?
- 31
- 93
- 279
Resolución
Respuesta correcta: c) 279
Para resolver este problema, primero calculamos la cantidad de agua que fluye por minuto, y luego usamos esa información para determinar cuánto tiempo tardará en llenarse la cisterna. Vamos paso a paso:

Por lo tanto, se tardará aproximadamente 279 minutos en llenar la cisterna, lo que coincide con la opción C que proporcionaste.
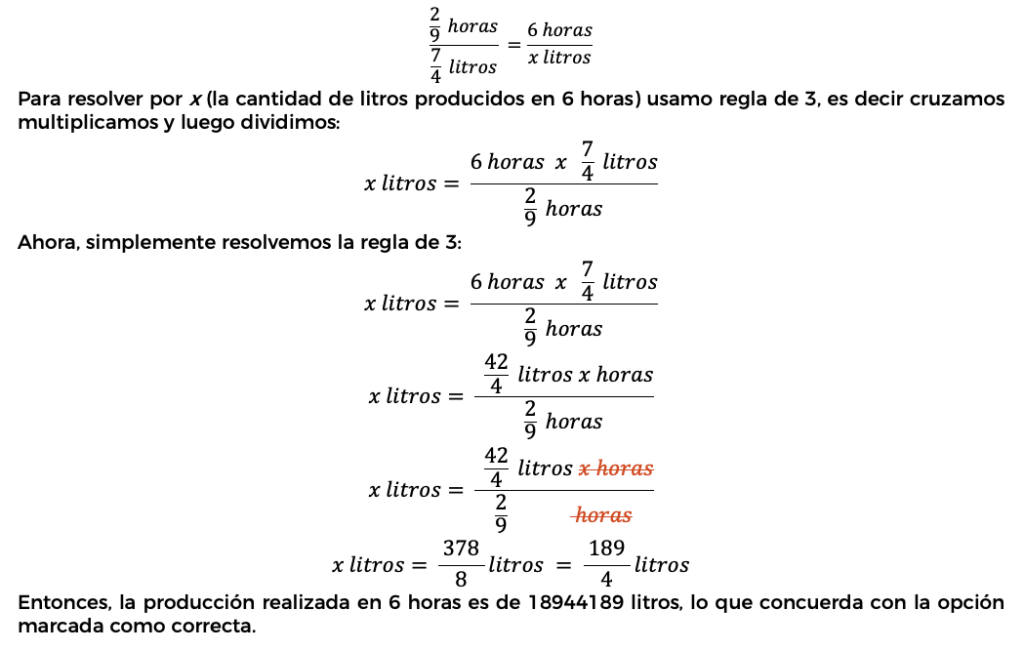
22. Identifique la producción realizada en 6 horas.
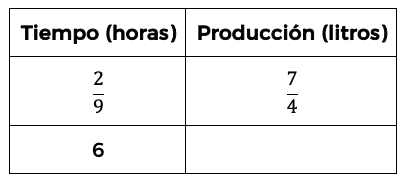
189/4
7/108
16/21
Resolución
Respuesta correcta: a) 189/4
Para identificar la producción realizada en 6 horas con los datos proporcionados en la tabla, usaremos una regla de tres simple directa. La tabla indica que en 2992 horas se producen 7447 litros. Queremos saber cuántos litros se producen en 6 horas. Vamos a establecer la proporción y resolverla:
Problemas con números racionales: Variaciones
23. Un hombre depositó $30,000 en un banco a un plazo de 5 años. Al término del periodo, retiró $48,000, los cuales corresponden al capital inicial más el interés. Identifique la tasa de interés simple anual que pagó el banco.
- 12%
- 32%
- 60%
Resolución
Respuesta correcta: a) 12%

24. En una población se detecta un nuevo virus en 8 personas. Al realizar los estudios pertinentes, la razón de crecimiento de infectados es de 2 cada 6 días. Después de 36 días, ¿Cuántos serán los infectados?
- 96
- 256
- 512
Resolución
Respuesta correcta: b) 256
Para resolver este problema, necesitamos calcular el número de infectados después de 36 días, sabiendo que el virus se propaga de manera que la cantidad de infectados se duplica cada 6 días. Esto es un ejemplo clásico de crecimiento exponencial, y lo modelaremos como una progresión geométrica.

Recomendaciones finales
Para que tu práctica en este simulador sea realmente efectiva:
- Aplica la jerarquía de operaciones: siempre resuelve primero paréntesis, luego exponentes, después multiplicaciones/divisiones y al final sumas/restas.
- No subestimes lo básico: muchos fallan por errores en signos, fracciones o porcentajes.
- Trabaja con límite de tiempo: simula las condiciones reales del examen.
- Analiza tus errores: cada equivocación es una oportunidad para reforzar conceptos.
- Refuerza con material extendido: en Pasatuexam tendrás acceso a explicaciones paso a paso, más reactivos resueltos y tips prácticos para aumentar tu velocidad.
Comienza gratis con este simulador de Aritmética y, si quieres tener acceso a todos los temas y garantizar un estudio completo, desbloquea el curso completo de Pasatuexam. Así tendrás la seguridad de que estás cubriendo todo lo necesario para ingresar a la universidad de tus sueños de forma más sencilla.
🚀 ¡Potencia tu Preparación con Nuestro Plan Profesional! 🎓
Si has empezado a descubrir cómo prepararte para el EXANI-II con nuestro contenido gratuito, ¡te felicitamos! 🌟 Pero, ¿estás listo para dar el gran salto? Con nuestro Plan Profesional, no solo vas un paso adelante, ¡vas a volar! 🚀
Al elegir el Plan Profesional, desbloquearás acceso a:
- Contenido sin Publicidad y sin Interrupciones 🚫: Estudia con la máxima concentración, sin anuncios que te distraigan de tus objetivos.
- Contenido de Calidad 100% Basado en las Guías del EXANI-II 📚: Confía en un material que sigue fielmente el currículo oficial, maximizando tu eficacia en el estudio.
- Lecciones Escritas y Videos Explicativos 📝🎥: Visualiza conceptos complejos con materiales diseñados para facilitar tu aprendizaje.
- Explicaciones Paso a Paso 📘: Todo se entiende mejor con nuestros métodos sencillos y claros.
- Preguntas Como en el Examen ❓: Practica con ejercicios que te preparan de verdad, aumentando tu seguridad al máximo.
- Simuladores de Examen 💻: Siente el día del examen antes de llegar, para que nada te sorprenda.
- Acceso Multiplataforma 📱💻: Aprende cuando quieras y desde cualquier dispositivo, facilitando tu preparación en todo momento.
Asegura tu acceso al éxito con el Plan Profesional. No es solo preparación, es tu boleto para lograr tus sueños universitarios. ¡Decídete ya! 🌈 No dejes pasar esta oportunidad. ⏳ ¡El tiempo vuela y tu futuro te espera!
🌟 Simulador Gratis 🌟
Si estás curioso sobre lo que el Plan Profesional puede ofrecerte, te tenemos una sorpresa. Haz clic aquí y enfrenta nuestro simulador especial. Con solo 30 preguntas, podrás medir qué tan preparado estás para tu examen de admisión. 🎯
Esta es tu oportunidad de obtener un vistazo de la calidad y profundidad que nuestro Plan Profesional tiene para ofrecer, y al mismo tiempo, evaluar tu nivel actual de preparación. 💪

