El simulador de Probabilidad y Estadística del EXANI-II es una de las herramientas más completas que el Ceneval ofrece para que los aspirantes practiquen. Este módulo mide tu capacidad para analizar información, interpretar datos, calcular probabilidades y comprender distribuciones estadísticas.
Al resolver este simulador encontrarás ejercicios de:
- Fundamentos de estadística: población, muestra y tipos de variables.
- Frecuencias y representaciones gráficas.
- Medidas descriptivas: media, moda, mediana, varianza y desviación estándar.
- Elementos de probabilidad: conjuntos y eventos.
- Cálculo de probabilidades con experimentos, distribuciones y combinaciones.
- Distribuciones estadísticas: binomial, normal y Bernoulli.
Para ayudarte, hemos dividido las preguntas del simulador en los temas específicos que corresponden, de manera que identifiques rápidamente en qué parte de la teoría debes reforzar.
👉 Algunos de estos temas podrás revisarlos gratis directamente en esta página, mientras que otros son parte del curso completo de Pasatuexam. Con él tendrás acceso a explicaciones detalladas, ejemplos paso a paso y tips estratégicos para dominar cada sección del examen.
📌 Ejercicios del simulador
Estadística: Fundamentos: población, muestra y tipos de variables
1. En una heladería se realiza una encuesta para conocer la satisfacción de sus clientes sobre los productos que ofrece. Una de las preguntas es acerca del sabor del helado y las posibles respuestas son “muy bueno”, “bueno”, “regular” y “malo”. ¿Qué tipo de variable estadística corresponde a las posibles respuestas?
- Ordinal
- Nominal
- Discreta
Resolución:
La pregunta de la encuesta se refiere al sabor del helado, y las opciones de respuesta son “muy bueno”, “bueno”, “regular” y “malo”. Estas respuestas representan una escala de satisfacción que tiene un orden inherente, de mejor a peor. Esto es lo que define a una variable ordinal. Cada término indica un nivel de satisfacción que es superior o inferior al otro, pero no sabemos exactamente cuánto superior o inferior es. Por ejemplo, la diferencia en la satisfacción entre “muy bueno” y “bueno” puede no ser la misma que entre “bueno” y “regular”. La respuesta correcta a la pregunta es “Ordinal” porque refleja esta jerarquía natural o ranking entre las categorías.
Las otras opciones son incorrectas por las siguientes razones:
- “Nominal”: Una variable nominal categoriza sin un orden inherente. Si las opciones de respuesta no tuvieran un orden de satisfacción claro (por ejemplo, sabores de helado como “chocolate”, “vainilla”, “fresa”), entonces sería nominal.
- “Discreta”: Se refiere a variables numéricas que toman valores contables o enteros específicos, lo cual no es el caso de las categorías descriptivas de satisfacción.
2. Para conocer la calidad de los tomates en un plantío de 10 hectáreas, el dueño decide recolectar 100 unidades de 2 hectáreas para su análisis. A las 100 unidades se les llama…
- Censo
- Población
- Muestra
Resolución:
En el segundo escenario, se recolectan 100 unidades de tomate de 2 hectáreas de un plantío de 10 hectáreas para analizar la calidad. Estas 100 unidades son un subconjunto de la población total de tomates y, por lo tanto, constituyen una “muestra”. Se utiliza una muestra porque es impracticable o imposible estudiar toda la población, que en este caso serían todos los tomates de las 10 hectáreas. La muestra debe ser representativa de la población para que las inferencias hechas a partir de ella sean válidas para la población completa.
Las otras opciones son incorrectas por las siguientes razones:
- “Censo”: Se refiere a un estudio que incluye a cada miembro de la población, que serían todos los tomates del plantío.
- “Población”: Se refiere a la totalidad de los sujetos o elementos que poseen la característica común que se desea estudiar. En este caso, la población sería la totalidad de los tomates en las 10 hectáreas, no solo las 100 unidades seleccionadas.
Estadística: Frecuencias y sus representaciones
3. Calcule el valor de x en la tabla de frecuencias, donde N = 44.
| Equipamiento de un auto | f | fr |
| Austero | 4 | x |
| Estándar | 22 | 0.50 |
| Lujoso | 18 | 0.41 |
- 0.02
- 0.09
- 0.18
Resolución:
La frecuencia relativa (fr) se calcula dividiendo la frecuencia absoluta de una categoría entre el total de observaciones. En este caso, para el equipamiento “Austero” con una frecuencia absoluta de 4, se divide 4 entre 44, lo que da 0.0909. Al redondear, se obtiene 0.09. Esto representa el 9% de los autos con equipamiento austero en relación con el total de 44 autos.
Respuesta correcta: 0.09
4. Para llevar el registro de una enfermedad, de un total de 74 personas, se recabaron los datos de personas infectadas por día y se elaboró la siguiente gráfica. ¿Cuál es la frecuencia acumulada en porcentaje, de personas infectadas, hasta antes del cuarto día?
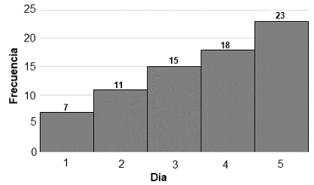
- 20 %
- 45 %
- 69 %
Resolución:
La frecuencia acumulada se obtiene sumando las frecuencias de todos los días anteriores hasta un punto determinado. En este caso, para calcular la frecuencia acumulada hasta antes del cuarto día, sumamos las frecuencias relativas de los tres primeros días y las multiplicamos por 100 para obtener el porcentaje.
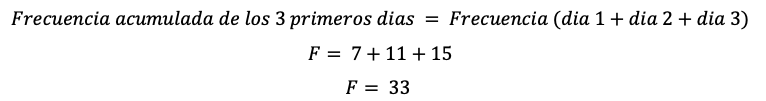
La frecuencia acumulada para los 3 primeros dias es de 33. Ahora debemos dividir 33 entre 74 y multiplicar el resultado por 100 para obtener el valor en porcentaje:
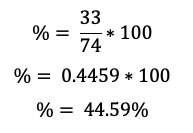
Por lo tanto, la suma de las frecuencias relativas de los tres días, convertida en porcentaje, da un total del 45%.
Respuesta correcta: 45%
5. En una fábrica de refrigeradores se registraron las unidades vendidas durante 15 días: 9, 10, 11, 8, 9, 10, 10, 7, 4, 15, 9, 8, 8, 6 y 14. ¿Cuál es la frecuencia relativa para 8 unidades vendidas?
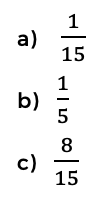
Resolución:
La frecuencia relativa se calcula dividiendo el número de veces que aparece un valor específico (en este caso, 8 unidades vendidas) entre el total de observaciones (15 días). Hay 3 ocurrencias de 8 unidades vendidas, por lo que la frecuencia relativa es 3/15, que se simplifica a 1/5 o 20%.
Esto indica que en el 20% de los días registrados se vendieron 8 unidades.
Respuesta correcta: 3/15 = 1/5
6. Identifique el tipo de frecuencia presentado en la columna z.
| x | y | z |
| 1 | 7 | 7 |
| 2 | 4 | 11 |
| 3 | 5 | 16 |
| 4 | 7 | 23 |
| 5 | 9 | 32 |
- Absoluta
- Relativa
- Acumulada
Resolución:
La columna z muestra las frecuencias acumuladas. Esto se deduce porque cada valor en z es la suma de su valor actual en y más todos los valores anteriores de y. Por ejemplo, 7 (primer valor) seguido de 7 + 4 = 11, luego 11 + 5 = 16, y así sucesivamente.
Esto es característico de una frecuencia acumulada, donde cada punto representa la suma de las frecuencias hasta ese punto.
7. ¿En cuál de los siguientes gráficos se utiliza una medida de frecuencia absoluta?
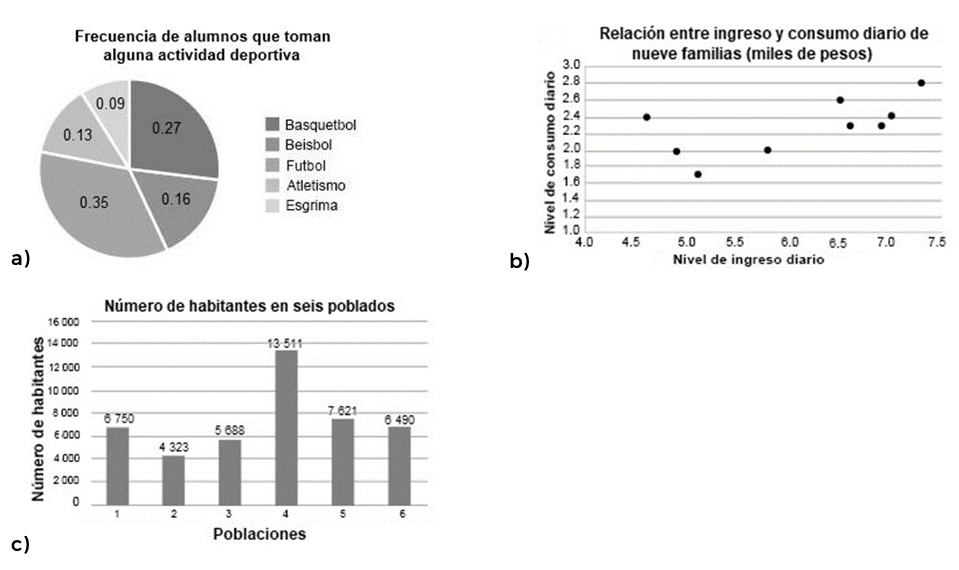
Resolución:
Para identificar el gráfico que utiliza una medida de frecuencia absoluta, debemos buscar el gráfico que muestra conteos o cantidades directas de las observaciones en lugar de proporciones o porcentajes.
- Gráfico a) Es un gráfico de pastel o circular que muestra las proporciones de alumnos que toman diferentes actividades deportivas. Cada porción del pastel representa una frecuencia relativa de la categoría correspondiente, no una frecuencia absoluta.
- Gráfico b) Muestra una relación entre dos variables cuantitativas: ingreso y consumo diario. Las posiciones de los puntos indican valores específicos, pero no hay conteos o frecuencias directas involucrados.
- Gráfico c) Es un gráfico de barras que muestra el número de habitantes en seis poblados. Las alturas de las barras representan conteos directos de habitantes, que son frecuencias absolutas.
Por lo tanto, el gráfico que utiliza una medida de frecuencia absoluta es el gráfico c), ya que muestra el conteo directo del número de habitantes en diferentes poblaciones.
Estadística: Medidas descriptivas
8. La tabla muestra la distribución de frecuencia del número de piezas producidas por 100 trabajadores de una fábrica. Calcule la media de los datos.
| Límite de clase | Frecuencia absoluta | Marca de clase |
| 31-40 | 16 | 35.5 |
| 41-50 | 18 | 45.5 |
| 51-60 | 31 | 55.5 |
| 61-70 | 21 | 65.5 |
| 71-80 | 14 | 75.5 |
| Total | 100 |
- 20.0
- 55.4
- 55.5
Resolución:
La media se calcula sumando las multiplicaciones de las frecuencias absolutas por las marcas de clase correspondientes y dividiendo el total por la suma de las frecuencias.
Las marcas de clase se calculan sumando el rango de la clase y dividiendolo entre 2.
Para la primera clase:

Haremos esto con todas las marcas de clase, pero podemos omitir esto al agregar 10 puntos a cada marca de clase, por ejemplo, la 2da marca de clase seria 45.5.
La formula para la media aritmetica con datos agrupados es:
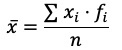
Aquí, la fórmula sería:
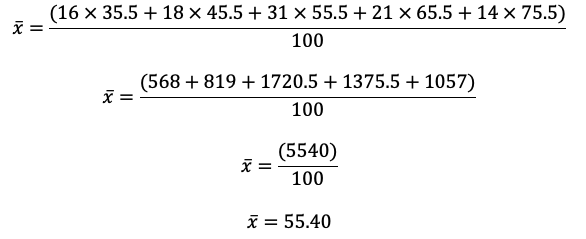
Esta es la media ponderada de los datos.
9. Calcule el percentil 30 de los datos. 0.8, 1.2, 1.5, 0.7, 0.5, 0.6, 0.9, 1.0, 1.3, 0.1
Considere:
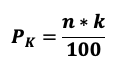
- 0.6
- 1.2
- 1.5
Resolución:
Primero, los datos se ordenan de menor a mayor.
0.1, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.2, 1.3, 1.5
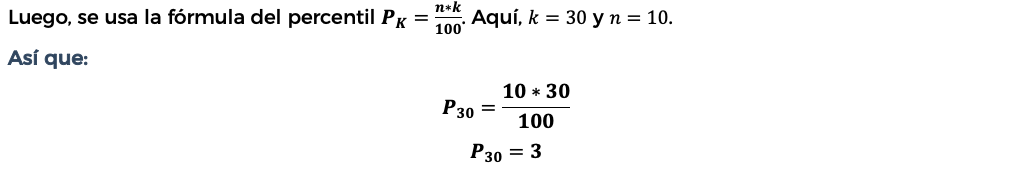
10. Calcule la varianza de la cantidad de alumnos encuestados en 5 grupos de una escuela, si la cantidad de cada grupo fue 21, 27, 26, 29 y 19.
- 4.2
- 17.8
- 24.4
Resolución:
La varianza se calcula utilizando la fórmula para muestras:
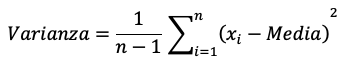
Aquí, calculamos primero la media:
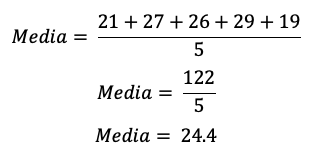
Ahora aplicamos la fórmula de la varianza, lo que nos da:

11. En un estudio de mercado se registra la cantidad de dinero, en pesos, que los clientes gastan en un supermercado. Se eligieron 5 al azar cuyos gastos fueron 252, 259, 261, 248 y 255. ¿Cuál es el valor de la desviación estándar de las cantidades gastadas?
- 5.2
- 10.5
- 27.5
Resolución:
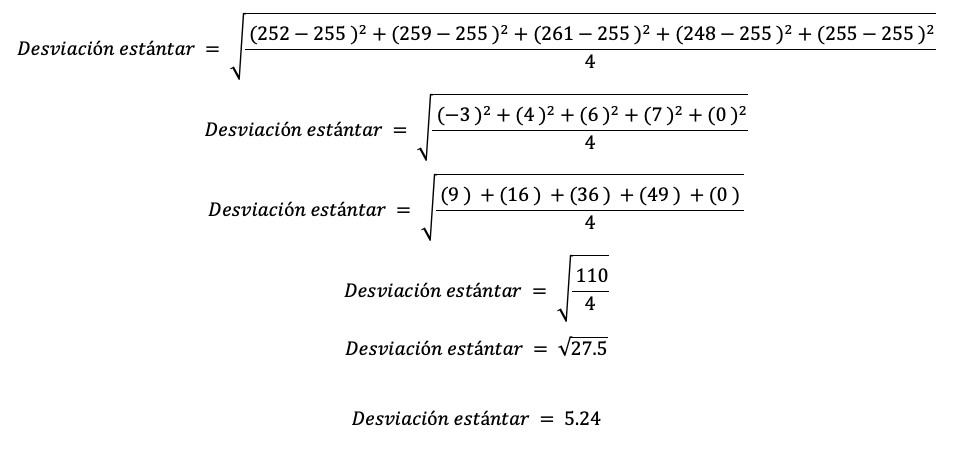
La desviación estándar se calcula tomando la raíz cuadrada de la varianza. Es decir:

Primero se calcula la media:
Ahora podemos utilizar nuestra formula de desviación estándar:
12. Determine la moda de los datos obtenidos en un estudio socioeconómico aplicado a 15 familias, en el cual se preguntó por el número de habitaciones que tienen en casa y se obtuvieron los siguientes resultados.
7, 3, 2, 3, 3, 6, 3, 7, 6, 6, 8, 4, 3, 8, 7
- 3
- 5
- 6
Resolución:
La moda es el valor que aparece con mayor frecuencia en un conjunto de datos. Al ordenar los datos del estudio socioeconómico, se observa que el número 3 aparece con mayor frecuencia (cinco veces), lo que lo convierte en la moda del conjunto de datos.
Probabilidad: Elementos: conjuntos y eventos
13. Se lanzan 2 dados sin importar el orden y se registran sus caras. El evento A consiste en obtener un número par de la suma de estas, mientras que el B en lograr un número menor que 10 de la suma de sus caras. ¿Cuál es la intersección de los 2 eventos?
- {(1, 1), (2, 2), (3, 3), (4, 4)}
- {1, 1), (1, 3), (1, 5), (2, 2), (2, 4), (2, 6), (3, 1), (3, 3), (3, 5), (4, 2), (4, 4), (5, 1), (5, 3), (6, 2)}
- {(1, 1), (1, 3), (1, 5), (2, 2), (2, 4), (2, 6), (3, 3), (3, 5), (4, 4)}
Resolución:
En este problema, queremos encontrar la intersección de dos eventos:
- Evento A: Obtener una suma par de dos dados.
- Evento B: Obtener una suma menor que 10 de dos dados.
Para encontrar la intersección de manera eficiente, podemos descartar rápidamente aquellos resultados que no cumplen con al menos uno de los dos criterios en cada una de las opciones. Analizaremos cada opcion:
- Opción a) Sólo incluye pares de números iguales. Si bien todos ellos tienen sumas pares y menores a 10, esta opción no incluye otras combinaciones que también cumplen con ambos criterios. Por lo tanto, es incompleta.
- Opción b) Esta opción incluye todas las combinaciones de las opciones posibles, pero se repiten datos y como en el problema se nos dice que no importa el orden de los dados un resultado de (1,3) es el mismo resultado que (3,1), por lo tanto, se estan repitiendo opciones y estamos dando importancia al orden en en que cae cada dado, asi que se descarta como opcion correcta .
- Opción c) Aqui todas estas combinaciones cumplen con ambos criterios, ademas no se repiten combinaciones con en la opcion b. Por lo tanto, esta opción es la opcion correcta.
14. El evento A se define como obtener una esfera azul de una urna, y P(A) = 0.30, mientras que el evento B se determina como lograr sol en el lanzamiento de una moneda cargada, y P(B) = 0.45. Si estos eventos son independientes, calcule P(A ∩ B).
- 0
- 0.135
- 0.75
Resolución:
Aquí estamos hablando de eventos independientes, dos eventos son independientes si la ocurrencia de uno no afecta la probabilidad del otro. En este caso, obtener una esfera azul de una urna (evento A) y lograr sol en un lanzamiento de moneda (evento B) son claramente independientes, ya que uno no influye en el resultado del otro.
La probabilidad de que ambos eventos, A y B, ocurran simultáneamente (es decir, la intersección de A y B) se calcula multiplicando las probabilidades de cada evento. Matemáticamente, esto se expresa como:
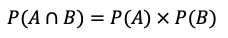
Dado que P(A) = 0.30 (30% de probabilidad de sacar una esfera azul) y P(B) = 0.45 (45% de probabilidad de que salga sol en la moneda), la probabilidad de que ambos eventos ocurran juntos es:

15. En una urna hay 52 esferas numeradas del 1 al 13 y clasificadas en 4 colores distintos. Si se extrae una de estas, ¿cuál es la probabilidad de obtener el número 4 o el 7, sin importar el color?
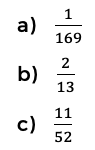
Resolución:
Tenemos una urna con 52 esferas. Cada esfera está numerada del 1 al 13, y hay esferas de 4 colores distintos. Esto implica que cada número del 1 al 13 se repite en 4 esferas de colores diferentes. Se pide calcular la probabilidad de sacar una esfera con el número 4 o el número 7, sin importar el color.
Entonces consideremos:
- Espacio Muestral (S): En problemas de probabilidad, el espacio muestral representa el conjunto total de resultados posibles. En este caso, el espacio muestral incluye 52 esferas diferentes.
- Evento de Interés (E): Nuestro evento de interés es sacar una esfera con el número 4 o 7. Necesitamos determinar cuántas esferas cumplen con esta condición.
- Fórmula de Probabilidad: La probabilidad de un evento se calcula como el número de resultados favorables dividido entre el número total de resultados posibles en el espacio muestral. Matemáticamente, se expresa como:
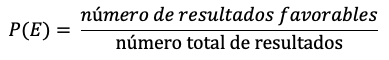
Número Total de Resultados (Espacio Muestral): 52 esferas en total.
Resultados Favorables para el Evento E: Hay 4 esferas con el número 4 y 4 esferas con el número 7, ya que cada número se repite en 4 colores distintos. Esto nos da un total de 8 esferas que son favorables para nuestro evento (4 esferas del número 4 y 4 esferas del número 7).
Cálculo de Probabilidad:

Probabilidad: Cálculo de la probabilidad
16. ¿Cuántas placas con 3 dígitos y 1 letra se pueden formar sin considerar el 0 ni la letra ñ? Considere que es posible formar placas con dígitos repetidos.
- 755
- 13 104
- 18 954
Resolución:
- Dígitos Disponibles: Como no se considera el 0, tenemos 9 dígitos posibles (1-9).
- Letras Disponibles: Excluyendo la ñ, tenemos 26 letras (alfabeto español completo).
- Posibilidades para Cada Dígito: Cada dígito puede ser cualquiera de los 9 (dígitos repetidos permitidos).
Tenemos 4 digitos, 4 de los cuales 3 son de numeros y 1 es de letras. Entonces:
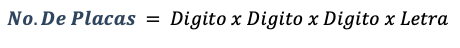
Entonces:
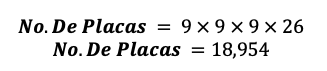
Entonces se pueden formar 18,954 placas diferentes.
17. Un diseñador terminó de elaborar 1 cartel y tiene disponibles 12 colores para iluminarlo. ¿Cuántas combinaciones obtiene si solo utiliza 5 colores diferentes, sin importar el orden?
- 792
- 95 040
- 248 832
Resolución:
Este tipo de problema habla de combinaciones como en su pregunta lo dice. La fórmula de combinaciones es:
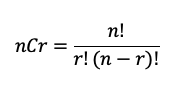
Donde:
- Número Total de Elementos (n): 12 colores.
- Número de Elementos a Seleccionar (r): 5 colores.
Sustituyendo nuestros datos en la formula tenemos:
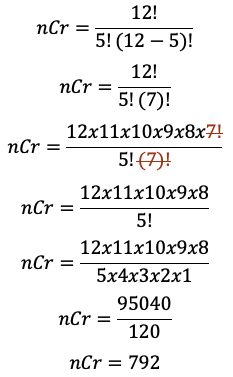
En conclusión, el diseñador puede obtener 792 combinaciones diferentes.
18. Se lanza 1 moneda, se tira 1 dado de 6 caras y se elige 1 carta de una baraja que contiene 40. Determine el espacio muestral.
- 3
- 240
- 480
Resolución:
En este ejercicio utilizamos el principio fundamental de conteo, el cual establece que si un evento puede ocurrir de maneras y otro evento independiente puede ocurrir de n maneras, entonces ambos eventos juntos pueden ocurrir de m x n maneras, en este caso tenemos 3 eventos independientes, por lo tanto Moneda (M) x Dado (D) x Baraja (B).
- Evento 1 (Moneda): 2 posibilidades (cara o cruz).
- Evento 2 (Dado): 6 posibilidades (1 a 6).
- Evento 3 (Baraja): 40 posibilidades (40 cartas diferentes).
Cálculo del Espacio Muestral:
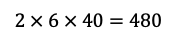
El espacio muestral de estos tres eventos combinados es 480.
19. ¿Cuál es la probabilidad de acertar la combinación de un candado cuya contraseña es 0613 si los dígitos que puede tener son del 0 al 6 y no se permiten repeticiones?
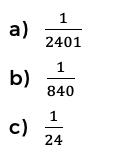
Resolución:
Aquí se trata de una permutación sin repetición con 7 dígitos disponibles (0, 1, 2, 3, 4, 5, 6) y una combinación de 4 dígitos,
La fórmula es:
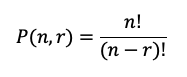
Donde n es 7 y r es 4. Entonces:
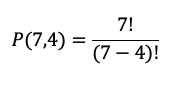
Calculando:

Entonces, la probabilidad es entonces 1/840.
Probabilidad: Distribuciones
20. Una propiedad de la curva de la distribución normal es que…
- su moda coincide con su media y su mediana
- sirve para conocer el número de éxitos en cierto número de intentos
- es útil en eventos impredecibles
Resolución:
La distribución normal es una curva simétrica en forma de campana. Esta simetría significa que la curva es un espejo de sí misma en ambos lados de un punto central. En el contexto de la distribución normal, este punto central es la media (promedio) de la distribución.
Media, Mediana y Moda:
- Media: La media es el promedio de todos los valores en la distribución. En una distribución normal, la media divide la curva en dos mitades iguales.
- Mediana: La mediana es el valor medio que divide el conjunto de datos en dos partes iguales. En una distribución normal, el 50% de los valores están por debajo de la mediana y el 50% por encima.
- Moda: La moda es el valor que ocurre con mayor frecuencia en el conjunto de datos. En una distribución normal, la moda es el pico de la curva de campana.
En una distribución normal, debido a la perfecta simetría de la curva, la media, la mediana y la moda son todas iguales y se encuentran en el mismo punto en el centro de la distribución. Este punto es también el máximo de la curva, lo que significa que la moda (el valor más frecuente) es igual a la media y la mediana.
¿Por qué las otras opciones son incorrectas?
- “Sirve para conocer el número de éxitos en cierto número de intentos”: Esta descripción es más adecuada para la distribución binomial, no para la normal.
- “Es útil en eventos impredecibles”: Aunque la distribución normal puede usarse en el análisis de eventos aleatorios, esta afirmación es demasiado vaga y no describe una propiedad específica de la curva de la distribución normal.
21. La distribución del ingreso diario por familia de una pequeña ciudad se representa por una variable aleatoria x, con una media de 500 y una desviación estándar de 75. ¿Cuál es el valor z estandarizado correspondiente a x = 610?
- 0.696
- 1.070
- 1.466
Resolución:
La distribución Z, o distribución normal estandarizada, transforma los datos de una distribución normal a una escala donde la media es 0 y la desviación estándar es 1. Esto se hace para poder comparar datos de diferentes distribuciones normales o para facilitar el cálculo de probabilidades.
La puntuación Z se calcula usando la fórmula:
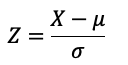
Aquí, X es el valor de interés, μ es la media de la distribución original, y σ es la desviación estándar de la distribución original. En este caso, se nos da que μ=500 y σ=75. Queremos calcular el valor Z para X=610. Entonces:
Sustituimos en la fórmula:
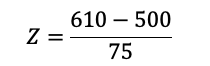
Realizando el Cálculo:
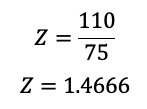
Un valor Z de 1.466 significa que el valor X=610 está aproximadamente 1.466 desviaciones estándar por encima de la media de la distribución. Esto nos da una idea de cómo se compara el valor específico con respecto a la distribución general.
22. Un experimento tipo Bernoulli tiene asociada una probabilidad de éxito p = 0.83, cuando n = 1. ¿Cuál es la varianza de x?
- 0.14
- 0.17
- 0.66
Resolución:
Un experimento de Bernoulli es un experimento aleatorio que tiene solo dos posibles resultados: “éxito” y “fracaso”. En este tipo de experimento, la probabilidad de éxito (p) y la probabilidad de fracaso (1-p) son constantes.
Como se explico mas arriba, en el tema, la varianza de una distribución de Bernoulli se calcula con la fórmula:
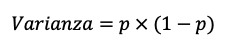
Aquí, p es la probabilidad de éxito.
Dado que p = 0.83, sustituimos en la fórmula:
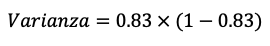
Ahora realizamos los calculos:

Este valor a menudo se redondea para facilitar su uso, en este caso a 0.14.
La varianza en un experimento de Bernoulli mide cuánto se espera que varíen los resultados del experimento respecto a la probabilidad de éxito. Una varianza de 0.14 sugiere una variabilidad moderada en torno a la probabilidad de éxito de 0.83.
23. ¿Con qué tipo de distribución se determina la probabilidad de obtener x número de aciertos al contestar al azar un examen de opción múltiple con n número de preguntas?
- Bernoulli
- Normal
- Binomial
Resolución:
El escenario descrito es un ejemplo clásico de un experimento que puede ser modelado con una distribución binomial. En un examen de opción múltiple, cada pregunta es un ensayo independiente con dos posibles resultados: acierto (éxito) o fallo (fracaso).
La distribución binomial se aplica a una serie de ensayos independientes (en este caso, las preguntas del examen) donde cada ensayo tiene solo dos posibles resultados. La probabilidad de éxito (por ejemplo, elegir la respuesta correcta) se asume constante en cada ensayo y la distribución binomial calcula la probabilidad de obtener un número específico de éxitos (en este caso, respuestas correctas) en un número fijo de ensayos.
Entonces, la respuesta correcta es una distribucion binomial. Las otras respuestas las descartamos debido a que:
- Bernoulli: Una distribución de Bernoulli se aplica a experimentos con solo dos resultados pero en un solo ensayo. No es adecuada para modelar una serie de ensayos, como un examen completo.
- Normal: La distribución normal es una distribución continua y se utiliza para modelar fenómenos que no son discretos, lo que no es aplicable al escenario de un examen de opción múltiple con un número fijo de preguntas.
24. En un laboratorio se tiene en observación un conjunto de plantas que se estima presenta una extraña característica genética con probabilidad de 0.7. Para realizar un análisis se eligen 5 plantas al azar y se define la variable aleatoria X, la cual indica el número de plantas que presentan la extraña característica. Determine la probabilidad de que en la elección la planta 3 presente dicha característica.
Considere para su cálculo la fórmula de la función de distribución:
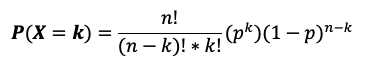
Resolución:
Este es un problema de distribución binomial, donde estamos interesados en encontrar la probabilidad de un número específico de éxitos (en este caso, plantas con una característica genética) en una serie de ensayos independientes (la selección de las plantas).
- La probabilidad de éxito (la planta presenta la característica) es p = 0.7.
- El número de ensayos (número de plantas seleccionadas) es n = 5.
Como queremos encontrar la probabilidad de exactamente 3 éxitos (k = 3), es decir, 3 plantas con la característica genética. La fórmula para la distribución binomial es:
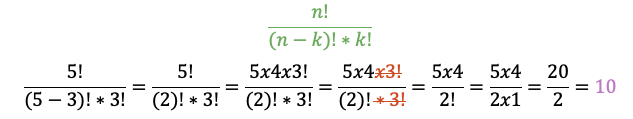
Aplicamos la fórmula:

Como ya tenemos nuestra distribucion binomial=10.
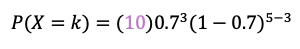
Ahora resolviendo:
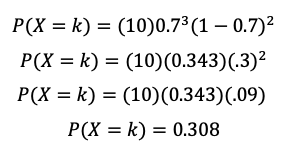
Hay aproximadamente un 30.8% de probabilidad de que exactamente 3 de las 5 plantas seleccionadas al azar presenten la característica genética.
✅ Recomendaciones finales
Estudiar Probabilidad y Estadística requiere práctica constante. Aquí tienes algunas recomendaciones:
- Domina lo básico antes de avanzar: conceptos como media, moda, mediana y varianza son recurrentes.
- Practica con tablas y gráficas: suelen aparecer ejercicios donde debes calcular frecuencias y representarlas.
- Aplica el principio fundamental de conteo: es clave en problemas de combinaciones y permutaciones.
- Haz simulaciones bajo tiempo real: así entrenas la rapidez que necesitarás en el examen.
- Aprende a identificar distribuciones: binomial, normal y Bernoulli son parte de los temas más buscados.
Con Pasatuexam puedes profundizar mucho más, acceder a material premium y resolver todas tus dudas con ejemplos prácticos. Así tendrás la seguridad de alcanzar el puntaje que necesitas y quedar en la universidad de tus sueños.
👉 Empieza gratis hoy mismo y desbloquea el curso completo cuando estés listo para llevar tu preparación al siguiente nivel.
🚀 ¡Potencia tu Preparación con Nuestro Plan Profesional! 🎓
Si has empezado a descubrir cómo prepararte para el EXANI-II con nuestro contenido gratuito, ¡te felicitamos! 🌟 Pero, ¿estás listo para dar el gran salto? Con nuestro Plan Profesional, no solo vas un paso adelante, ¡vas a volar! 🚀
Al elegir el Plan Profesional, desbloquearás acceso a:
- Contenido sin Publicidad y sin Interrupciones 🚫: Estudia con la máxima concentración, sin anuncios que te distraigan de tus objetivos.
- Contenido de Calidad 100% Basado en las Guías del EXANI-II 📚: Confía en un material que sigue fielmente el currículo oficial, maximizando tu eficacia en el estudio.
- Lecciones Escritas y Videos Explicativos 📝🎥: Visualiza conceptos complejos con materiales diseñados para facilitar tu aprendizaje.
- Explicaciones Paso a Paso 📘: Todo se entiende mejor con nuestros métodos sencillos y claros.
- Preguntas Como en el Examen ❓: Practica con ejercicios que te preparan de verdad, aumentando tu seguridad al máximo.
- Simuladores de Examen 💻: Siente el día del examen antes de llegar, para que nada te sorprenda.
- Acceso Multiplataforma 📱💻: Aprende cuando quieras y desde cualquier dispositivo, facilitando tu preparación en todo momento.
Asegura tu acceso al éxito con el Plan Profesional. No es solo preparación, es tu boleto para lograr tus sueños universitarios. ¡Decídete ya! 🌈 No dejes pasar esta oportunidad. ⏳ ¡El tiempo vuela y tu futuro te espera!
🌟 Simulador Gratis 🌟
Si estás curioso sobre lo que el Plan Profesional puede ofrecerte, te tenemos una sorpresa. Haz clic aquí y enfrenta nuestro simulador especial. Con solo 30 preguntas, podrás medir qué tan preparado estás para tu examen de admisión. 🎯
Esta es tu oportunidad de obtener un vistazo de la calidad y profundidad que nuestro Plan Profesional tiene para ofrecer, y al mismo tiempo, evaluar tu nivel actual de preparación. 💪

