El estudio de la estadística es esencial para el éxito en la sección de pensamiento matemático del EXANI-II. Este temario aborda dos aspectos fundamentales de la estadística descriptiva: las frecuencias y la representación gráfica de información. Comprender estos conceptos es crucial para analizar y sintetizar datos, habilidades clave evaluadas en el examen.
- El enfoque en frecuencias permite entender cómo se distribuyen los datos en un conjunto, identificando tendencias y patrones. Aprenderemos a construir y analizar tablas de frecuencia, lo que es vital para interpretar correctamente los datos.
- La representación gráfica, por otro lado, es esencial para visualizar y comunicar información estadística de manera efectiva. Abordaremos diferentes tipos de gráficos y cómo interpretarlos, una habilidad directamente relevante para las preguntas del EXANI-II.
› Frecuencias
Existen tres tipos principales de frecuencias que se utilizan para describir y analizar datos:
Frecuencia Absoluta (f )
La frecuencia absoluta es simplemente el conteo del número de veces que aparece un valor en un conjunto de datos. Por ejemplo, si tenemos una encuesta en una clase de 30 estudiantes sobre el número de hermanos que tienen, podemos tener la siguiente tabla de frecuencia absoluta:
| Número de hermanos | Frecuencia Absoluta |
| 0 | 5 |
| 1 | 12 |
| 2 | 8 |
| 3 | 3 |
| 4 | 2 |
Aquí, el valor f para los estudiantes sin hermanos es 5, lo que significa que 5 estudiantes reportaron no tener hermanos.
Frecuencia Relativa (fr )
La frecuencia relativa se calcula dividiendo la frecuencia absoluta de cada valor entre el número total de observaciones. Se suele expresar en porcentaje o en decimales donde la suma de todas las frecuencias relativas es igual a 1. Siguiendo con el ejemplo anterior, la tabla con frecuencia relativa sería:
| Número de hermanos | Frecuencia Absoluta | Frecuencia Relativa |
| 0 | 5 | 0.1667 (16.67%) |
| 1 | 12 | 0.4000 (40.00%) |
| 2 | 8 | 0.2667 (26.67%) |
| 3 | 3 | 0.1000 (10.00%) |
| 4 | 2 | 0.0667 (6.67%) |
Para calcular la frecuencia relativa del valor “1 hermano”, dividimos 12 (la frecuencia absoluta) entre 30 (el total de estudiantes), obteniendo 0.4, que se expresa como 40%.
Frecuencia Acumulada (F )
La frecuencia acumulada es la suma de las frecuencias absolutas para todos los valores hasta el valor actual. Continuando con el mismo conjunto de datos, la tabla sería:
| Número de hermanos | Frecuencia Absoluta | Frecuencia Relativa | Frecuencia Acumulada |
| 0 | 5 | 0.1667 (16.67%) | 5 |
| 1 | 12 | 0.4000 (40.00%) | 17 |
| 2 | 8 | 0.2667 (26.67%) | 25 |
| 3 | 3 | 0.1000 (10.00%) | 28 |
| 4 | 2 | 0.0667 (6.67%) | 30 |
La frecuencia acumulada para “hasta 2 hermanos” es 25, lo que significa que 25 de los 30 estudiantes tienen 2 o menos hermanos.
Interpretación de la Tabla
La tabla completa nos ofrece una imagen clara de la distribución de la cantidad de hermanos entre los estudiantes encuestados. Podemos observar que la mayoría de los estudiantes tiene 1 hermano, y que muy pocos tienen 4 hermanos. La frecuencia relativa nos permite entender la proporción de cada categoría en relación con el total, y la frecuencia acumulada nos muestra cómo se suman los datos a medida que avanzamos a través de las categorías.
› Representación gráfica de información
Las frecuencias se pueden representar tanto en tablas como en gráficos, cada uno con su propio propósito y método de interpretación. A continuación, se detalla cómo crear y entender estas representaciones.
Tablas de Frecuencia
Una tabla de frecuencia organiza los datos y sus correspondientes frecuencias (absoluta, relativa y acumulada) de manera que se puedan observar y comparar fácilmente.
| Número de hermanos | Frecuencia Absoluta | Frecuencia Relativa | Frecuencia Acumulada |
| 0 | 5 | 0.1667 (16.67%) | 5 |
| 1 | 12 | 0.4000 (40.00%) | 17 |
| 2 | 8 | 0.2667 (26.67%) | 25 |
| 3 | 3 | 0.1000 (10.00%) | 28 |
| 4 | 2 | 0.0667 (6.67%) | 30 |
La tabla resultante proporciona una visión completa de cómo se distribuyen los datos y su relevancia proporcional.
Gráficos de pastel
Los gráficos de pastel, también conocidos como gráficos circulares, son representaciones visuales que muestran cómo se dividen o distribuyen los datos en categorías. Cada segmento del círculo (o “rebanada”) representa la frecuencia relativa de cada categoría. A continuación, se describe cómo crear un gráfico de pastel:
- Calcula las Frecuencias Relativas: Antes de dibujar un gráfico de pastel, necesitas conocer la frecuencia relativa de cada categoría en tu conjunto de datos. Esto se hace dividiendo la frecuencia absoluta de cada categoría entre el total de datos y se expresa como un porcentaje.
- Convierte las Frecuencias Relativas en Ángulos: Cada porcentaje se convertirá en un ángulo del círculo del gráfico de pastel. Como un círculo completo tiene 360 grados, cada porcentaje se multiplica por 3.6 para obtener el ángulo correspondiente. Por ejemplo, si una categoría representa el 25% de los datos, su ángulo será de 90 grados (25% * 360° = 90°).
- Dibuja el Círculo y Segmentos: Dibuja un círculo y usa un transportador para medir y dibujar cada segmento del pastel basado en los ángulos calculados.
- Colorea y Etiqueta Cada Segmento: Asigna un color distinto a cada segmento y coloca una etiqueta que indique la categoría que representa, junto con su porcentaje correspondiente.

Histogramas
Un histograma es un tipo de gráfico de barras que representa la distribución de frecuencias de datos numéricos continuos. En este grafico se utilizan frecuencias absolutas. Los pasos para crear un histograma son:
- Determinar intervalos de clase: Se divide el rango total de los datos en intervalos llamados clases.
- Contar frecuencias por intervalo: Se cuenta cuántos datos caen dentro de cada intervalo de clase.
- Dibujar barras: En el eje horizontal se colocan los intervalos de clase y en el eje vertical las frecuencias absolutas. Se dibuja una barra para cada intervalo cuya altura representa la frecuencia.
Los histogramas son útiles para visualizar la forma de la distribución de los datos, como la simetría, la asimetría y la presencia de picos.

Polígonos de Frecuencia
Un polígono de frecuencia es una representación gráfica que conecta los puntos representativos de las frecuencias de los intervalos en un histograma. Para dibujar un polígono de frecuencia:
- Identificar puntos medios: Se localizan los puntos medios de la parte superior de cada barra del histograma.
- Conectar puntos: Se conectan estos puntos con líneas rectas.
El polígono de frecuencia es útil para comparar diferentes distribuciones de frecuencias, especialmente si se superponen varios polígonos en el mismo eje.

Ojivas
La ojiva es un gráfico que muestra la frecuencia acumulada. Los pasos para construir una ojiva son:
- Determinar puntos de frecuencia acumulada: Se toman los valores de la frecuencia acumulada de la tabla de frecuencia.
- Marcar puntos en el gráfico: Se coloca en el eje horizontal el límite superior de cada intervalo y en el eje vertical la frecuencia acumulada correspondiente.
- Conectar puntos: Se unen los puntos con líneas rectas.
Las ojivas permiten determinar rápidamente cuántos datos caen por debajo de un cierto valor y son útiles para encontrar percentiles y cuartiles en la distribución de los datos.
Vídeo Resumen
Preguntas EXANI-II
Pregunta 1 (Ejercicio tomado del Simulador EXANI-II):
En la tabla se presenta información referente a tres municipios de México: el número aproximado de habitantes y el número de casos activos de covid-19 (personas enfermas) al 11 de agosto de 2020.
De acuerdo con los datos, ¿en qué municipio el número de casos activos es mayor por cada 1 000 habitantes?
| Municipio | Población aproximada (habitantes) | Número de casos activos de covid-19 |
| Guadalajara, Jalisco | 1 503 000 | 443 |
| Naucalpan de Juárez, Estado de México | 755 000 | 437 |
| Monclova, Coahuila | 245 000 | 369 |
a. Guadalajara, Jalisco
b. Naucalpan de Juárez, Estado de México
c. Monclova, Coahuila
Explicación
Respuesta correcta: c) Monclova, Coahuila. Para determinar en qué municipio el número de casos activos de Covid-19 es mayor por cada 1,000 habitantes, se debe calcular la tasa de casos activos por cada 1,000 habitantes. Esto se hace dividiendo el número de casos activos por la población total de cada municipio y luego multiplicando el resultado por 1,000. Para Monclova, Coahuila, el cálculo es 369245,000×1,000245,000369×1,000, que resulta en aproximadamente 1.5 casos por cada 1,000 habitantes, siendo el valor más alto entre los tres municipios.
Pregunta 2 (Ejercicio tomado del Simulador EXANI-II):
Se realizó un estudio acerca de los niveles de triglicéridos con los grupos de personas que acudieron a diversos laboratorios clínicos a realizarse una prueba de sangre. Sobre uno de los laboratorios clínicos se comentó: “Las personas en promedio tienen un nivel de triglicéridos de 135 mg/dL de sangre; sin embargo, el número de personas con los mismos niveles de triglicéridos es muy variable. Así como hay muchas con un nivel de triglicéridos alrededor de 45 mg/dL, otro tanto casi igual presenta niveles altos cercanos a 225 mg/dL”.
¿Qué gráfica representa la descripción anterior?
a) 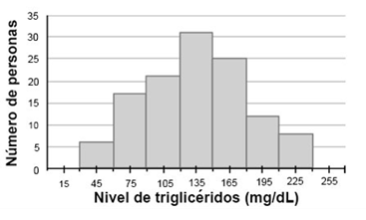 | b) 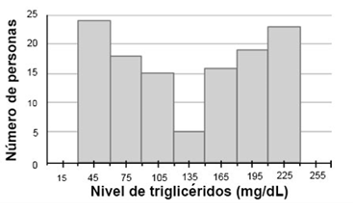 | c) 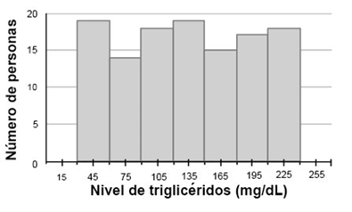 |
Explicación
Respuesta correcta: Grafica B. La descripción indica que hay una gran variabilidad en los niveles de triglicéridos, con muchas personas en los extremos bajos (cerca de 45 mg/dL) y altos (cerca de 225 mg/dL), y menos personas en el nivel promedio (135 mg/dL). Esto sugiere una distribución bimodal, donde los datos se agrupan significativamente en dos diferentes puntos extremos. La gráfica que mejor representa esta situación es la B, debido a que muestra dos picos pronunciados en los extremos y menos frecuencia en el medio, reflejando la variabilidad y la distribución bimodal de los datos.
Pregunta 3 (Ejercicio tomado del Simulador EXANI-II):
Considerando la siguiente gráfica, complete el enunciado para que represente una situación equilibradamente beneficiosa entre la oferta, la demanda y la tendencia de compra actual.
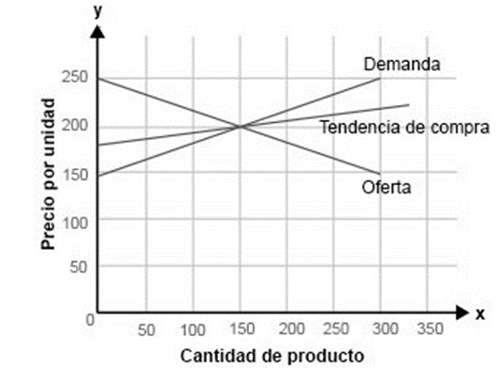
Al elaborar ___ productos, se tiene un costo de ___ por cada uno de ellos.
a. 150, $200
b. 300, $150
c. 300, $250
Explicación
Respuesta correcta: a) “150, $200”. Como podemos ver en la grafica, el punto donde las líneas de oferta, demanda y tendencia de compra se intersectan parece estar alrededor de 150 unidades en la cantidad de producto y 200 en el costo, basándonos en las opciones proporcionadas y la ubicación aproximada de la intersección en el gráfico, la opción a) “150, $200” es la correcta.
Pregunta 4 (Ejercicio tomado del Simulador EXANI-II):
El siguiente gráfico de barras representa el número de días que esperaron los clientes que llamaron a una empresa telefónica para solucionar un problema con su celular.
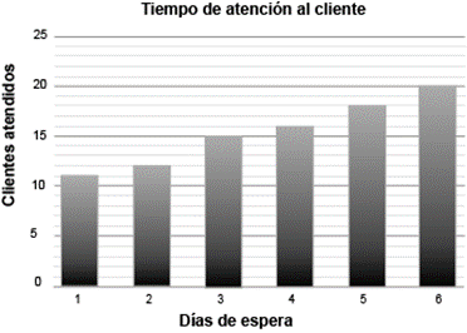
¿Cuál gráfico circular representa de manera equivalente la información?
a)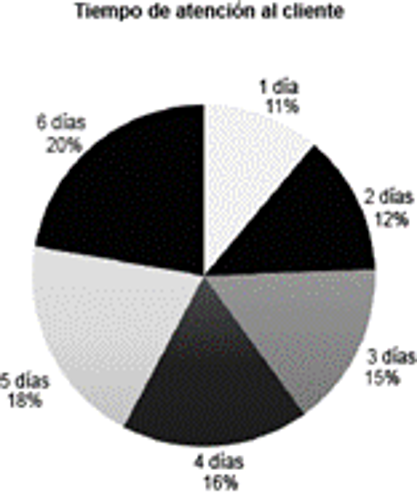 | b) 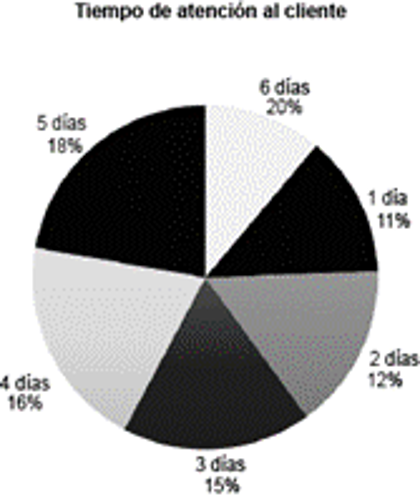 | c) 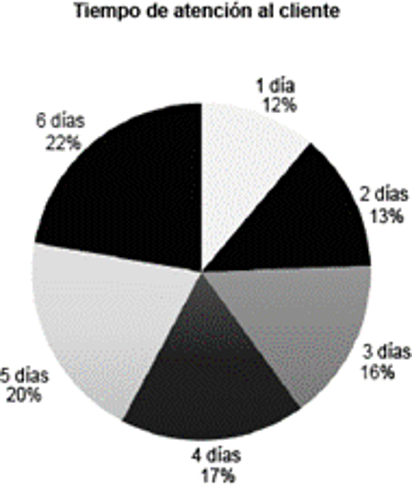 |
Explicación:
Respuesta correcta: c. Si observamos las 3 opciones disponibles, se observa que la opción c es la que mejor representa la misma información que el gráfico de barras inicial. Esto se debe a que en la opción c, las proporciones de cada sector del gráfico circular corresponden adecuadamente con las frecuencias relativas de los datos presentados en el gráfico de barras. Dado que el total de datos es 100, cada unidad en el gráfico de barras se traduce directamente en un porcentaje en el gráfico circular. Así, la distribución de los clientes según los días de espera se refleja de manera precisa en la opción c, tanto numéricamente como visualmente, garantizando una representación fiel de los datos originales en el gráfico de barras
🚀 ¡Potencia tu Preparación con Nuestro Plan Profesional! 🎓
Si has empezado a descubrir cómo prepararte para el EXANI-II con nuestro contenido gratuito, ¡te felicitamos! 🌟 Pero, ¿estás listo para dar el gran salto? Con nuestro Plan Profesional, no solo vas un paso adelante, ¡vas a volar! 🚀
Al elegir el Plan Profesional, desbloquearás acceso a:
- Contenido sin Publicidad y sin Interrupciones 🚫: Estudia con la máxima concentración, sin anuncios que te distraigan de tus objetivos.
- Contenido de Calidad 100% Basado en las Guías del EXANI-II 📚: Confía en un material que sigue fielmente el currículo oficial, maximizando tu eficacia en el estudio.
- Lecciones Escritas y Videos Explicativos 📝🎥: Visualiza conceptos complejos con materiales diseñados para facilitar tu aprendizaje.
- Explicaciones Paso a Paso 📘: Todo se entiende mejor con nuestros métodos sencillos y claros.
- Preguntas Como en el Examen ❓: Practica con ejercicios que te preparan de verdad, aumentando tu seguridad al máximo.
- Simuladores de Examen 💻: Siente el día del examen antes de llegar, para que nada te sorprenda.
- Acceso Multiplataforma 📱💻: Aprende cuando quieras y desde cualquier dispositivo, facilitando tu preparación en todo momento.
Asegura tu acceso al éxito con el Plan Profesional. No es solo preparación, es tu boleto para lograr tus sueños universitarios. ¡Decídete ya! 🌈 No dejes pasar esta oportunidad. ⏳ ¡El tiempo vuela y tu futuro te espera!
🌟 Simulador Gratis 🌟
Si estás curioso sobre lo que el Plan Profesional puede ofrecerte, te tenemos una sorpresa. Haz clic aquí y enfrenta nuestro simulador especial. Con solo 30 preguntas, podrás medir qué tan preparado estás para tu examen de admisión. 🎯
Esta es tu oportunidad de obtener un vistazo de la calidad y profundidad que nuestro Plan Profesional tiene para ofrecer, y al mismo tiempo, evaluar tu nivel actual de preparación. 💪
