Para asegurar un entendimiento completo del tema de “Sistemas de Ecuaciones Lineales con dos y tres incógnitas”, es esencial que como estudiantes se familiaricen con los conceptos fundamentales y las técnicas de resolución. Estos conocimientos son vitales para el éxito en el examen de admisión de pensamiento matemático del EXANI-II.
Un sistema de ecuaciones lineales consiste en dos o más ecuaciones que tienen varias incógnitas comunes. La resolución de estos sistemas implica encontrar el valor de las incógnitas de tal forma que satisfagan todas las ecuaciones del sistema simultáneamente. Un sistema de ecuaciones lineales con dos incógnitas se representa generalmente como:
1) 3x + 2y = 12
2) x – y = 1
Métodos de Resolución (Sustitución, Igualación, Reducción)
Hay varios métodos para resolver sistemas de ecuaciones, cada uno con sus propias ventajas en diferentes situaciones. Dominar estos métodos es crucial para su éxito en el examen de admisión de pensamiento matemático del EXANI-II.
Sustitución
Este método es útil cuando una de las ecuaciones en el sistema puede ser fácilmente despejada para una de las incógnitas. Una vez que una incógnita ha sido despejada, esa expresión se ‘sustituye’ en la otra ecuación, permitiendo que se resuelva para la segunda incógnita. Este método es particularmente eficiente cuando las ecuaciones están ya dispuestas para despejar una incógnita directamente. Ahora veamos un ejemplo utilizando este metodo, utilizaremos el siguiente sistema de dos incognitas:
1) 3x + 2y = 12
2) x – y = 1
Paso 1: Despejar una variable en una de las ecuaciones
Vamos a despejar x en la ecuación 2:
x – y = 1
x = y + 1
Paso 2: Sustituir la variable despejada en la otra ecuación
Sustituimos x en la ecuación 1:
3x + 2y = 12
3(y + 1) + 2y = 12
Paso 3: Resolver para la variable restante
3(y + 1) + 2y = 12
3y + 3 + 2y = 12
5y + 3 = 12
5y = 12 – 3
5y = 9
y = 9/5
Paso 4: Sustituir el valor obtenido en la ecuación despejada
Usamos el valor de y en la ecuación despejada para encontrar x:
x = 9/5 + 1
x = 9/5 + 5/5
x = 14/5
Igualación
La igualación es un método que consiste en despejar la misma incógnita en ambas ecuaciones. Una vez que las dos expresiones para esa incógnita son iguales, puedes igualar las expresiones resultantes y resolver para la otra incógnita. Este método es efectivo cuando es sencillo despejar la misma incógnita de ambas ecuaciones. Ahora veamos un ejemplo utilizando este metodo, utilizaremos el siguiente sistema de dos incognitas:
1) 3x + 2y = 12
2) x – y = 1
Paso 1: Despejar la misma variable en ambas ecuaciones
Despejamos y en ambas ecuaciones.
En la ecuación 2, despejamos y:
x – y = 1
y = x – 1
Ahora despejamos y en la ecuación 1:
3x + 2y = 12
2y = 12 – 3x

Paso 2: Igualar ambas expresiones para y

Paso 3: Resolver para la variable restante
Multiplicamos todo por 2 para deshacernos del denominador:
2x – 2 = 12 – 3x
Sumamos 3x a ambos lados y sumamos 2 a ambos lados:

Paso 4: Sustituir el valor obtenido en una de las expresiones despejadas

Reducción o Eliminación
El método de reducción implica manipular las ecuaciones para que, al sumarlas o restarlas, una de las incógnitas se elimine, dejando una sola ecuación con una sola incógnita. Esto se logra a menudo multiplicando las ecuaciones por factores que hacen que los coeficientes de una de las incógnitas sean iguales en magnitud pero opuestos en signo. Ahora veamos un ejemplo utilizando este metodo, utilizaremos el siguiente sistema de dos incognitas:
1) 3x + 2y = 12
2) x – y = 1
Paso 1: Preparar las ecuaciones para la eliminación
Multiplicamos la ecuación 2 por 2 para igualar los coeficientes de y:
2) x – y = 1
2x – 2y = 2
Paso 2: Sumar o restar las ecuaciones para eliminar una variable
Sumamos esta nueva ecuación a la ecuación 1:
1) 3x + 2y = 12
(3x + 2y) + (2x – 2y) = 12 + 2
5x = 14
Paso 3: Resolver para la variable restante

Paso 4: Sustituir el valor obtenido en una de las ecuaciones originales
Usamos la ecuación 2 para encontrar y:

Multiplicamos todo por 5 para deshacernos del denominador:
14 – 5y = 5
Restamos 14 en ambos lados:
– 5y = 5 – 14
5y = -9
Dividimos entre -5:

Análisis de Soluciones Gráficas
El análisis de soluciones gráficas es una herramienta poderosa para entender los sistemas de ecuaciones lineales. Vamos a analizar gráficamente el mismo sistema de ecuaciones que resolvimos anteriormente para ilustrar cómo se hace este proceso.
El sistema es:
1) 3x + 2y = 12
2) x – y = 1
Paso 1: Graficar la primera ecuación
Para graficar la ecuación 3x+2y=12, primero resolveremos para y cuando x=0 y para x cuando y=0.
- Si x=0:
3(0)+2y=12
2y=12
y=6
- Si y=0:
3x+2(0)=12
3x=12
x=4
Esto nos da dos puntos: (0, 6) y (4, 0). Podemos dibujar una línea a través de estos dos puntos.
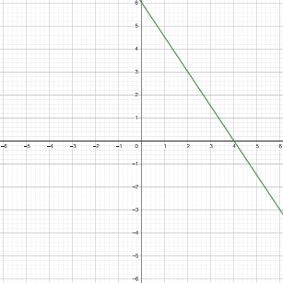
Todos los puntos por los que pasa la linea verde son posibles soluciones para la primera ecuacion. Pero debemos buscar el unico sitio donde se pueden solucionar las dos ecuaciones del sistema y para obtener estos valores de x y y debemos graficar la segunda ecuacion.
Paso 2: Graficar la segunda ecuación
Para graficar la ecuación x−y=1, haremos lo mismo y encontraremos los puntos donde corta a los ejes.
- Si x=0:
0-y=1
y=-1
- Si y=0:
x-0=1
x=1
Esto nos da otros dos puntos: (0, -1) y (1, 0). Dibujamos una línea a través de estos dos puntos.
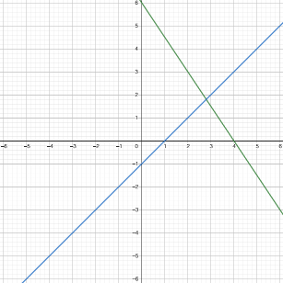
Paso 3: Encontrar el punto de intersección
El punto donde estas dos líneas se cruzan es la solución al sistema de ecuaciones. De nuestros cálculos anteriores, ya sabemos que la solución es x=14/5 y y=9/5, o en forma decimal, x=2.8 y y=1.8. Este punto debería caer en la intersección de las dos líneas que hemos graficado.
Paso 4: Comprobar la solución gráficamente
Dibujamos ambas líneas en un sistema de coordenadas cartesianas y verificamos que efectivamente se cortan en el punto (2.8, 1.8).
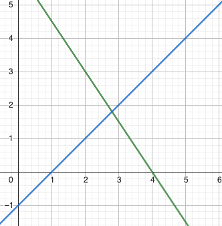
El análisis gráfico nos permite ver que:
- Si las dos líneas se cortan en un punto, el sistema es consistente y determinado, lo que significa que hay una única solución.
- Si las dos líneas son paralelas y distintas, el sistema es inconsistente, lo que significa que no hay solución.
- Si las dos líneas son coincidentes, el sistema es consistente y indeterminado, lo que significa que hay infinitas soluciones.
Ahora, en una situación de examen como el EXANI-II, se podría presentar una gráfica con líneas ya dibujadas, y se pediría al estudiante que identificara el punto de intersección, o se podría pedir que clasifique el sistema basado en una gráfica proporcionada. Este tipo de análisis visual es crucial para responder de manera efectiva y eficiente a las preguntas del examen de admisión.
Vídeo Resumen
Preguntas EXANI-II
Pregunta 1 (Ejercicio tomado del Simulador EXANI-II):
¿Cuál es la solución de la ecuación 4q – r = 12?
a. Una posible solución es q = 1, r = -8
b. No tiene solución
c. La única solución es q = 1, r = -8
Explicación:
Respuesta correcta: a) Una posible solución es q = 1, r = -8. Una ecuación lineal con dos variables, como 4q – r = 12, tiene infinitas soluciones. La respuesta proporcionada (q = 1, r = -8) es solo una de las muchas soluciones posibles. Para que una solución sea válida, debe satisfacer la ecuación cuando sustituimos las variables por los valores dados. En este caso, si sustituimos q con 1 y r con -8, obtenemos 4(1) – (-8) = 4 + 8 = 12, lo cual es verdadero.
Pregunta 2 (Ejercicio tomado del Simulador EXANI-II):
La siguiente gráfica representa un sistema de 3 ecuaciones de 2 variables.
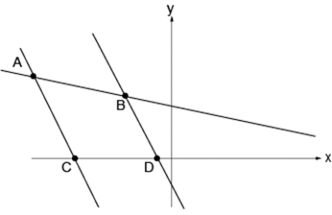
¿Cuál es la solución del sistema?
a. Los puntos C y D son solución
b. Los puntos A y B son solución
c. No tiene solución
Explicación:
Respuesta correcta: c) No tiene solución. Cuando tenemos un sistema de tres ecuaciones con dos incógnitas, es posible que no haya una solución única que satisfaga las tres ecuaciones simultáneamente, lo cual ocurre cuando las rectas representadas por las ecuaciones no se intersectan todas en un único punto. Si las rectas no se cruzan en un punto común, entonces el sistema no tiene solución. Esto se refiere a un sistema inconsistente, donde al menos una de las ecuaciones representa una recta que no intercepta el punto de intersección de las otras dos.
🚀 ¡Potencia tu Preparación con Nuestro Plan Profesional! 🎓
Si has empezado a descubrir cómo prepararte para el EXANI-II con nuestro contenido gratuito, ¡te felicitamos! 🌟 Pero, ¿estás listo para dar el gran salto? Con nuestro Plan Profesional, no solo vas un paso adelante, ¡vas a volar! 🚀
Al elegir el Plan Profesional, desbloquearás acceso a:
- Contenido sin Publicidad y sin Interrupciones 🚫: Estudia con la máxima concentración, sin anuncios que te distraigan de tus objetivos.
- Contenido de Calidad 100% Basado en las Guías del EXANI-II 📚: Confía en un material que sigue fielmente el currículo oficial, maximizando tu eficacia en el estudio.
- Lecciones Escritas y Videos Explicativos 📝🎥: Visualiza conceptos complejos con materiales diseñados para facilitar tu aprendizaje.
- Explicaciones Paso a Paso 📘: Todo se entiende mejor con nuestros métodos sencillos y claros.
- Preguntas Como en el Examen ❓: Practica con ejercicios que te preparan de verdad, aumentando tu seguridad al máximo.
- Simuladores de Examen 💻: Siente el día del examen antes de llegar, para que nada te sorprenda.
- Acceso Multiplataforma 📱💻: Aprende cuando quieras y desde cualquier dispositivo, facilitando tu preparación en todo momento.
Asegura tu acceso al éxito con el Plan Profesional. No es solo preparación, es tu boleto para lograr tus sueños universitarios. ¡Decídete ya! 🌈 No dejes pasar esta oportunidad. ⏳ ¡El tiempo vuela y tu futuro te espera!
🌟 Simulador Gratis 🌟
Si estás curioso sobre lo que el Plan Profesional puede ofrecerte, te tenemos una sorpresa. Haz clic aquí y enfrenta nuestro simulador especial. Con solo 30 preguntas, podrás medir qué tan preparado estás para tu examen de admisión. 🎯
Esta es tu oportunidad de obtener un vistazo de la calidad y profundidad que nuestro Plan Profesional tiene para ofrecer, y al mismo tiempo, evaluar tu nivel actual de preparación. 💪
