Las inecuaciones son elementos cruciales en el pensamiento matemático, ya que proporcionan una manera de expresar relaciones de desigualdad entre diferentes cantidades. Entender las inecuaciones es fundamental para quienes se preparan para exámenes de admisión, como el EXANI-II, donde el pensamiento matemático es evaluado con ejercicios que utilicen estos conceptos.
Inecuación para el EXANI-II
Una inecuación se define como una expresión matemática que establece que dos cantidades no son iguales en valor; indica que una es mayor o menor que la otra. Los símbolos utilizados para representar estas relaciones son fundamentales para el pensamiento matemático y son esenciales para resolver problemas en el EXANI-II. Estos símbolos incluyen < (menor que), > (mayor que), ≤ (menor o igual que) y ≥ (mayor o igual que).
Signos de las Inecuaciones
Los signos de inecuación son símbolos matemáticos utilizados para representar las relaciones de desigualdad entre dos expresiones. Son fundamentales en el ámbito del pensamiento matemático para describir cómo se comparan los valores numéricos.
Menor que (<)
Indica que el valor a la izquierda del signo es menor que el valor a la derecha.
- Cuándo usarlo: Cuando necesitas expresar que una cantidad es estrictamente menor que otra, sin incluir el valor con el que se compara. Ejemplo: x<5 significa que x puede tomar cualquier valor menor que 5, pero no 5.
Mayor que (>)
Señala que el valor a la izquierda del signo es mayor que el valor a la derecha.
- Cuándo usarlo: Para expresar que una cantidad es estrictamente mayor que otra, excluyendo el valor de comparación. Por ejemplo, x>3 indica que x puede ser cualquier valor mayor que 3, pero no 3.
Menor o igual que (≤)
Muestra que el valor a la izquierda del signo es menor que el valor a la derecha, o igual a este.
- Cuándo usarlo: Cuando es necesario indicar que una cantidad puede ser menor que otra o exactamente igual. Este signo se usa para incluir el valor de comparación en el conjunto de soluciones. Por ejemplo, x≤10 significa que x puede ser cualquier valor menor que 10, incluido el 10.
Mayor o igual que (≥)
Indica que el valor a la izquierda del signo es mayor que el valor a la derecha, o igual a este.
- Cuándo usarlo: Para expresar que una cantidad puede ser mayor que otra o igual a esta. Se utiliza para incluir el valor de comparación dentro del conjunto de soluciones posibles. Ejemplo: x≥4 sugiere que x puede tomar cualquier valor mayor o igual a 4.
Comparación entre Ecuaciones e Inecuaciones
La diferencia clave entre ecuaciones e inecuaciones radica en que las ecuaciones expresan una igualdad exacta entre dos expresiones, mientras que las inecuaciones destacan una relación de desigualdad. Este concepto es vital en el pensamiento matemático y es un área de enfoque en el EXANI-II, donde se evalúa la capacidad para interpretar y resolver ambos tipos de expresiones matemáticas.
Tipos de Inecuaciones
En el pensamiento matemático, un enfoque detallado hacia los tipos de inecuaciones es esencial, especialmente para los estudiantes que se preparan para el EXANI-II, donde la comprensión profunda de estas puede ser decisiva. Las inecuaciones se clasifican según la relación que establecen entre las expresiones y el grado de las variables involucradas.
- Inecuaciones Lineales: Son las más básicas, con expresiones que forman una línea recta al graficarse. Se representan generalmente como ax + b < 0, ax + b > 0, ax + b <= 0, o ax + b >= 0, donde a y b son constantes, y x es la variable.
- Inecuaciones Cuadráticas: Involucran términos con la variable al cuadrado (x²). La forma general es ax² + bx + c < 0, ax² + bx + c > 0, ax² + bx + c <= 0, o ax² + bx + c >= 0, con a, b, y c como constantes. Su resolución puede requerir completar el cuadrado o aplicar la fórmula cuadrática.
- Inecuaciones Racionales: Presentan una mayor complejidad, con expresiones fraccionarias que tienen variables en el denominador. Resolverlas implica encontrar el dominio de la expresión racional y analizar los signos en diferentes rangos para determinar los intervalos de solución.
- Inecuaciones con Valor Absoluto: Miden la distancia de un número a cero, representadas como |ax + b| < c, |ax + b| > c, |ax + b| <= c, o |ax + b| >= c. Su resolución considera los casos en que la expresión dentro del valor absoluto es positiva o negativa, llevando a dos conjuntos de inecuaciones lineales para solucionar.
Cada tipo de inecuación requiere métodos específicos de solución y es esencial para el análisis matemático en diversos contextos, incluyendo el EXANI-II.
Inecuaciones Lineales (Lo que vendrá en el EXANI-II)
Las inecuaciones lineales constituyen un componente esencial del pensamiento matemático. Una inecuación lineal es una desigualdad que involucra expresiones lineales. Se caracteriza por tener una o más variables a la primera potencia y puede presentarse en diversas formas, tales como ax + b < c, ax + b > c, ax + b <= c, o ax + b >= c, donde a, b, y c son constantes reales y x es la variable. Estas expresiones definen una relación de desigualdad entre dos lados, indicando que uno es menor, mayor, menor o igual, o mayor o igual que el otro.
Solución de Inecuaciones Lineales
La solución de una inecuación lineal implica encontrar todos los valores posibles de x que hacen verdadera la desigualdad. Este proceso puede incluir técnicas como la simplificación algebraica y el uso de propiedades de inecuaciones para aislar la variable de interés. Un aspecto clave es la representación de estas soluciones, que puede ser en forma de intervalos o mediante representación gráfica en una recta numérica, ofreciendo una visualización clara del conjunto de soluciones.
Representación Gráfica de Soluciones
La representación gráfica de las soluciones de inecuaciones lineales en la recta numérica es una herramienta poderosa para visualizar el rango de valores que satisfacen la desigualdad. Esta técnica no solo ayuda a comprender el concepto de inecuación sino que también permite analizar y comparar de manera eficiente los conjuntos de solución.
Ejemplo de Ejercicio EXANI-II
Para ilustrar cómo resolver inecuaciones lineales, consideremos un problema práctico que podría encontrarse en un contexto real o ser similar a una pregunta en el EXANI-II dentro de la sección de pensamiento matemático.
Supongamos que estás organizando un evento y tienes un presupuesto máximo de $500 para gastar en decoraciones y comidas. Si las decoraciones ya costaron $200, ¿cuánto dinero puedes gastar en comida sin exceder tu presupuesto?
Representación con Inecuación Lineal
Para representar este problema con una inecuación, definamos x como el dinero que puedes gastar en comida. La suma del dinero gastado en decoraciones ($200) y el dinero que planeas gastar en comida (x) no debe exceder el presupuesto total ($500). Esto se puede representar mediante la siguiente inecuación lineal:
200 + x ≤ 500
Solución del Problema
Para resolver esta inecuación y encontrar el valor de x, seguimos los siguientes pasos:
1. Tenemos la siguiente inecuación:
200 + x ≤ 500
- Restamos $200 a ambos lados de la inecuación para aislar la variable x en un lado:
x ≤ 500 − 200
- Simplificamos la expresión en el lado derecho de la inecuación:
x ≤ 300
Interpretación de la Solución
La solución x≤300 significa que puedes gastar hasta $300 en comida para el evento sin exceder el presupuesto total de $500. Es importante destacar que cualquier cantidad de dinero en comida que sea menor o igual a $300 es aceptable según las restricciones del presupuesto.
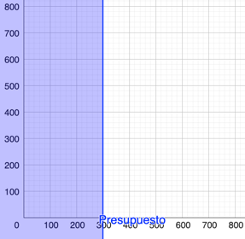
Representación Gráfica
Si quisiéramos representar la solución de esta inecuación en una recta numérica, marcaríamos un segmento que inicia en el origen (o en cualquier punto que represente el valor mínimo que podría gastarse, que podría ser $0 si consideramos que no es obligatorio gastar todo el presupuesto en comida) y se extiende hasta el punto que representa $300, incluyendo este último valor, indicando que todos los valores dentro de este rango son soluciones válidas de la inecuación.
Preguntas EXANI-II
Pregunta 1 (Ejercicio tomado del Simulador EXANI-II):
Identifique la inecuación que describe el siguiente fenómeno.
De acuerdo con la Ley Federal del Trabajo, una persona debe laborar como máximo 42 horas semanales en horario nocturno; es decir, a lo sumo 7.5 horas diarias para cumplir con esta jornada.
- x = 7.5
- x ≥ 7.5
- x ≤ 7.5
Resolución
La pregunta presentada es un ejemplo típico de cómo las inecuaciones lineales se utilizan para modelar situaciones reales en el contexto del EXANI-II, específicamente dentro de la sección de pensamiento matemático. El problema se basa en interpretar correctamente la legislación laboral para determinar la inecuación que describe adecuadamente las horas máximas de trabajo permitidas por la ley.
El enunciado menciona que, según la Ley Federal del Trabajo, una persona puede laborar hasta 42 horas semanales en horario nocturno, lo que se traduce en un máximo de 7.5 horas diarias. Esto implica que el número de horas trabajadas por día (x) no debe superar las 7.5 horas.
Las opciones proporcionadas son:
- x=7.5: Esta opción indica que la persona trabaja exactamente 7.5 horas todos los días, lo cual es una situación específica pero no abarca la flexibilidad permitida por la ley de trabajar menos horas.
- x≥7.5: Sugiere que la persona trabaja 7.5 horas o más, lo cual contradice la restricción máxima establecida por la ley.
- x≤7.5: Correcta. Esta inecuación refleja correctamente que la persona debe trabajar hasta 7.5 horas al día como máximo, cumpliendo así con la normativa laboral que permite trabajar menos de 7.5 horas pero no más.
La correcta interpretación de la ley y su aplicación a través de inecuaciones lineales es una habilidad evaluada en el EXANI-II. En este caso, la opción correcta es x≤7.5, ya que representa adecuadamente el límite máximo de horas de trabajo permitidas por día según la ley, ofreciendo así un modelo matemático exacto del escenario laboral descrito. Esta pregunta ilustra la importancia de entender y aplicar inecuaciones lineales en contextos legales y normativos, un aspecto crucial del pensamiento matemático en exámenes de admisión y en la vida real.
🚀 ¡Potencia tu Preparación con Nuestro Plan Profesional! 🎓
Si has empezado a descubrir cómo prepararte para el EXANI-II con nuestro contenido gratuito, ¡te felicitamos! 🌟 Pero, ¿estás listo para dar el gran salto? Con nuestro Plan Profesional, no solo vas un paso adelante, ¡vas a volar! 🚀
Al elegir el Plan Profesional, desbloquearás acceso a:
- Contenido sin Publicidad y sin Interrupciones 🚫: Estudia con la máxima concentración, sin anuncios que te distraigan de tus objetivos.
- Contenido de Calidad 100% Basado en las Guías del EXANI-II 📚: Confía en un material que sigue fielmente el currículo oficial, maximizando tu eficacia en el estudio.
- Lecciones Escritas y Videos Explicativos 📝🎥: Visualiza conceptos complejos con materiales diseñados para facilitar tu aprendizaje.
- Explicaciones Paso a Paso 📘: Todo se entiende mejor con nuestros métodos sencillos y claros.
- Preguntas Como en el Examen ❓: Practica con ejercicios que te preparan de verdad, aumentando tu seguridad al máximo.
- Simuladores de Examen 💻: Siente el día del examen antes de llegar, para que nada te sorprenda.
- Acceso Multiplataforma 📱💻: Aprende cuando quieras y desde cualquier dispositivo, facilitando tu preparación en todo momento.
Asegura tu acceso al éxito con el Plan Profesional. No es solo preparación, es tu boleto para lograr tus sueños universitarios. ¡Decídete ya! 🌈 No dejes pasar esta oportunidad. ⏳ ¡El tiempo vuela y tu futuro te espera!
🌟 Simulador Gratis 🌟
Si estás curioso sobre lo que el Plan Profesional puede ofrecerte, te tenemos una sorpresa. Haz clic aquí y enfrenta nuestro simulador especial. Con solo 30 preguntas, podrás medir qué tan preparado estás para tu examen de admisión. 🎯
Esta es tu oportunidad de obtener un vistazo de la calidad y profundidad que nuestro Plan Profesional tiene para ofrecer, y al mismo tiempo, evaluar tu nivel actual de preparación. 💪
