El módulo de Matemáticas Financieras en el EXANI-II es fundamental para quienes buscan ingresar a carreras relacionadas con administración, contaduría, economía o negocios. Este simulador está diseñado para que practiques con reactivos muy similares a los que encontrarás en el examen real, enfrentándote a problemas de razones, proporciones, porcentajes, intereses, amortizaciones y análisis financiero.
Cada pregunta está organizada por tema, de modo que podrás identificar a qué área corresponde cada reactivo y reforzar tu estudio de forma más enfocada. Algunos ejercicios estarán disponibles gratis, pero si deseas acceder a todas las explicaciones y prácticas extendidas, puedes desbloquear el curso completo en Pasatuexam y asegurar así una preparación mucho más sólida.
¿Qué mide este simulador?
El simulador de Matemáticas Financieras mide tu capacidad de análisis y resolución en:
- Razones y proporciones aplicadas a inversiones, ahorros y costos.
- Proporcionalidad directa e inversa en escenarios financieros y productivos.
- Cálculo de descuentos y rebajas, aplicado a precios reales.
- Porcentajes de aumento o reducción en bienes y servicios.
- Sucesiones y series como base de pagos e ingresos recurrentes.
- Interés simple y sus aplicaciones en inversiones, préstamos y amortizaciones.
- Tasa de interés y periodos de inversión, con resolución de problemas prácticos.
- Diferencias en pagos y saldos insolutos en créditos.
Estos temas son indispensables no solo para el examen, sino también como herramientas básicas para tu vida profesional en cualquier disciplina de las ciencias económico-administrativas.
SIMULADOR DE MATEMÁTICAS FINANCIERAS
Elementos Financieros Básicos: Razones
1. Si una persona tiene en el banco un saldo de $400, de los cuales una parte son ahorros y los otros intereses en una razón de 3:2, ¿cuál es la proporción representada?
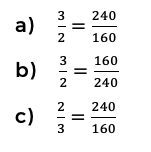
Resolución


Elementos Financieros Básicos: Proporciones Directas e Inversas
2. Una línea aérea oferta 320 lugares a un costo de $5,400 para obtener sus gastos. Si sólo vende 180 lugares, ¿a qué costo deberá tener el pasaje para cubrir los gastos?
- $3,037.50
- $8,437.50
- $9,600.00
Resolución
Para resolver este problema, primero debemos entender que los gastos totales de la línea aérea deben ser cubiertos por los ingresos obtenidos de la venta de boletos. Los gastos totales se mantienen constantes, independientemente de cuántos boletos se vendan. El objetivo es encontrar el nuevo precio por boleto cuando solo se venden 180 lugares, para cubrir los mismos gastos totales.
Los datos que tenemos son:

3. Para producir 3.5 toneladas de tela se paga un total de $2,450. Si se necesita producir 8 toneladas, ¿cuál es la proporción de la variación que representa los datos proporcionados?
- 3.5 es a 8 como $5,600 a $2,450
- 3.5 es a $2,450 como 8 es a $5,600
- 3.5 es a $5,600 como 8 es a $2,450
Resolución
Para resolver este problema, usaremos la regla de tres simple para encontrar la cantidad de dinero que se necesita para producir 8 toneladas de tela, basándonos en la relación proporcionada: producir 3.5 toneladas de tela cuesta $2,450.
La regla de tres simple se basa en una relación de proporcionalidad directa entre dos magnitudes. En este caso, la cantidad de tela y el costo asociado son directamente proporcionales. Esto significa que si se aumenta la cantidad de tela, el costo también aumenta en la misma proporción.
Los datos que tenemos son:

4. Calcule el monto actual de la inversión de una persona si al inicio tenía $218,000 y ha utilizado ![]() de la misma.
de la misma.
- $87,200
- $130,800
- $305,200
Resolución

5. Determine a cuánto asciende la deuda de una persona si el banco le prestó ![]() de $900,000, y ahora es
de $900,000, y ahora es ![]() menor que hace 5 meses.
menor que hace 5 meses.
- $150,000
- $450,000
- $1,050,000
Resolución

6. ¿Qué porcentaje representa el aumento en el precio por litro de gasolina que, al iniciar el año era de $14 y el incremento que se realizó es de $3?
- 0.42%
- 14.17%
- 21.43%
Resolución
Para calcular el porcentaje de aumento en el precio por litro de gasolina, seguimos el procedimiento que mencionas. Se divide el aumento en el precio, que es de $3, entre el precio inicial, que es de $14, y luego se multiplica el resultado por 100% para obtener el porcentaje. La fórmula es la siguiente:

Elementos Financieros Básicos: Descuentos
7. Calcule el precio total que se debe pagar por la compra de dos casas de campaña, cuyo precio de lista es de $55,499.00 cada una, considerando que hay una oferta que indica que al llevar dos, la segunda tiene una rebaja de 15%.
- $94,348.30
- $102,673.15
- $119,322.85
Resolución
Para resolver este problema, debemos calcular el precio total de la compra de dos casas de campaña, teniendo en cuenta la oferta que indica que al comprar dos, la segunda tiene un descuento del 15%. Vamos a desglosar el cálculo paso a paso:

8. Obtenga el monto de la rebaja en la compra de 1 computadora con precio inicial de $38,000.00 y que se ofrece en tienda con un 15%.
- $2,533.33
- $5,700.00
- $32,300.00
Resolución
Para encontrar el monto de la rebaja en la compra de una computadora que tiene un precio inicial de $38,000.00 y se ofrece con un descuento del 15%, debemos seguir estos pasos:
- Convertir el porcentaje de descuento a su forma decimal: Para esto, dividimos el porcentaje de descuento entre 100. En este caso, 15% se convierte en 0.15 (15 ÷ 100 = 0.15).
- Calcular el monto del descuento: Multiplicamos el precio inicial de la computadora por el porcentaje de descuento en forma decimal. Entonces, $38,000.00 × 0.15.
- Realizar la multiplicación: Al hacer la operación 38,000 × 0.15 obtenemos el monto del descuento.
Ahora, realicemos la multiplicación para encontrar la respuesta:
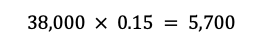
Por lo tanto, el monto de la rebaja en la compra de la computadora es de $5,700.00.
9. ¿Cuál es el precio final de una vacuna cuyos insumos de producción equivalen a $1,213.00 y el laboratorio proyecta una ganancia de 25%?
- $1,238.00
- $1,261.52
- $1,516.25
Resolución
Para calcular el precio final de una vacuna, tomando en cuenta el costo de los insumos de producción y el porcentaje de ganancia proyectado por el laboratorio, seguimos estos pasos:
- Convertir el porcentaje de ganancia a su forma decimal: Al igual que con el descuento, convertimos el porcentaje a decimal dividiendo por 100. En este caso, 25% se convierte en 0.25 (25 ÷ 100 = 0.25).
- Sumar 1 al porcentaje de ganancia decimal: Esto se hace para calcular el multiplicador total que incluye el costo original más la ganancia. Por lo tanto, 1 + 0.25 = 1.25.
- Multiplicar el costo de los insumos por el multiplicador total: Esto nos da el precio final de la vacuna. Entonces, $1,213.00 × 1.25.
Ahora, realizamos la operación:
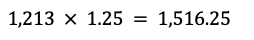
Por lo tanto, el precio final de la vacuna, incluyendo la ganancia proyectada del 25%, es de $1,516.25.
10. ¿Qué porcentaje de descuento se le aplica al sueldo de una persona que percibe $11,460, al cual se le cobra un préstamo personal, y recibe al final únicamente $10,300?
- 10.12%
- 11.26%
- 11.60%
Resolución
Para calcular el porcentaje de descuento aplicado al sueldo de una persona debido a un préstamo personal, seguimos estos pasos:
- Determinar la cantidad descontada del sueldo:
- Sueldo original: $11,460
- Sueldo después del préstamo: $10,300
- Calculamos la diferencia: $11,460 – $10,300 = $1,160
- Calcular el porcentaje que representa esta cantidad descontada respecto al sueldo original:
- Usamos la fórmula: (Cantidad descontada / Sueldo original) × 100
- Sustituimos los valores:

Por lo tanto, el porcentaje de descuento aplicado al sueldo debido al préstamo personal es aproximadamente 10.12%.
11. ¿Cuál era el costo original de un televisor, si su precio de mostrador es de $15,800 y ya incluye un descuento de 15%?
- $18,170.00
- $18,588.23
- $23,700.00
Resolución
Para resolver este problema, necesitamos encontrar el precio original del televisor antes del descuento del 15%. El precio después del descuento es de $15,800, lo cual representa el 85% del precio original (ya que el 100% menos el 15% de descuento nos da 85%).
Sabemos que el $15,800 es el 85% del costo original, porque este es el precio después de aplicar un descuento del 15%. Usamos la regla de tres simple. Si $15,800 corresponde al 85%, ¿cuánto corresponderá al 100%? La ecuación sería:
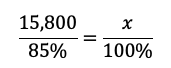
Aquí, x es el precio original del televisor que estamos buscando. Ahora unicamente despejamos x y obtenemos:
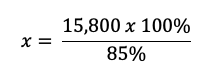
Sustituimos los porcentajes por su equivalente decimal (85% = 0.85, 100% = 1) y realizamos la operación:
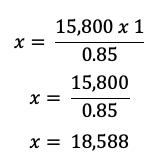
Entonces, el costo original del televisor era aproximadamente $18,588.
Elementos Financieros Básicos: Sucesiones y Series
12. Encuentre el cuarto término de la sucesión aritmética.
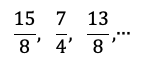
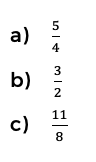
Resolución

13. Una empresa mayorista de papelería vende lápices con un precio inicial de $4.00. Por cada pieza extra disminuye 30 centavos, con un tope de compra de hasta 10 lápices. ¿Cuál es el precio que se paga por la octava pieza?
- $1.30
- $1.60
- $1.90
Resolución
Para calcular el precio del octavo lápiz, utilizaremos la fórmula para encontrar un término específico en una sucesión aritmética. Sabemos que el precio inicial es de $4.00 y que por cada lápiz adicional, el precio disminuye en 30 centavos ($0.30). Esto forma una sucesión aritmética donde cada término es el precio del lápiz correspondiente.
La fórmula para el n-ésimo término de una sucesión aritmética es:

Interés Simple: Elementos de Interés Simple y Amortización
14. ¿Cuánto es el saldo insoluto por pagar a los 3 meses sobre una deuda adquirida al comprar un equipo de cómputo de $46,200, con una facilidad de pago de 8 mensualidades y una tasa de 5% al mes? $28,875 $9,240 $18,480 $27,720
Resolución

15. Se compra una televisión a crédito con precio de $65,000.00. El plazo establecido para el pago es de 4 meses con una tasa mensual de 7% y montos de amortización fija por $16,250.00. Considerando la tabla, ¿cuál es el saldo insoluto del préstamo para el tercer mes?
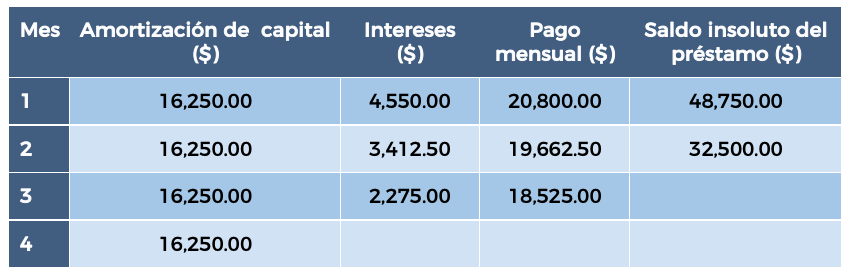
- $13,975.00
- $16,250.00
- $18,525.00
Resolución
El saldo insoluto es la cantidad que queda pendiente de pagar en un préstamo después de realizar un pago. En este caso, cada mes se amortiza una parte del capital y se pagan intereses. Para resolver este problema debemos:
- Revisar los datos proporcionados:
- Precio inicial del televisor (préstamo inicial): $65,000.00.
- Amortización fija mensual: $16,250.00.
- Saldo insoluto después del primer mes: $48,750.00.
- Saldo insoluto después del segundo mes: $32,500.00.
- Calcular el saldo insoluto para el tercer mes:
- El saldo insoluto después del segundo mes es de $32,500.00.
- La amortización fija para el tercer mes es de $16,250.00.
- Para calcular el saldo insoluto del tercer mes, restamos la amortización del tercer mes del saldo insoluto del segundo mes:

Por lo tanto, el saldo insoluto del préstamo para el tercer mes es de $16,250.00.
16. Determine la tasa de interés de una inversión que se colocó durante 1 mes con un capital inicial de $10,000 y un saldo final de $10,500.
- 1.05%
- 5.00%
- 95.24%
Resolución
Para determinar la tasa de interés de una inversión, se puede utilizar una variante de la fórmula del interés simple. El enfoque es calcular el interés basándose en la relación entre el capital final y el capital inicial. Tenemos los siguientes datos:
- Capital inicial: $10,000.
- Saldo final: $10,500.
- Tiempo de la inversión: 1 mes (aunque no es necesario para este cálculo).
- Utilizar la fórmula modificada para el interés:
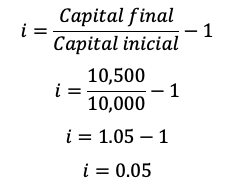
- Convertir la tasa de interés a un porcentaje:
- Multiplicar por 100 para obtener el porcentaje.
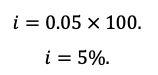
Por lo tanto, la tasa de interés de la inversión es del 5.00%.
17. ¿A qué tasa de interés anual un capital de $65,000 invertido en una cuenta bancaria produce un monto de $85,000 en 4 años?
- 5.23%
- 7.69%
- 30.77%
Resolución
Para calcular la tasa de interés anual que produce un monto específico en un periodo de tiempo determinado, podemos usar la fórmula del interés simple. Aunque el interés compuesto es comúnmente utilizado en cuentas bancarias, seguimos las instrucciones para usar la fórmula del interés simple:

Interés Simple: Inversiones
18. Si una persona desea invertir $40,000.00 en una cuenta de ahorros que ofrece una tasa de interés simple de 55% anual, ¿cuánto obtendrá al final en un plazo de 4 años?
- $62,000.00
- $128,000.00
- $230,880.25
Resolución
Para calcular cuánto obtendrá una persona al invertir en una cuenta de ahorros con interés simple, utilizamos la fórmula del interés simple para calcular el monto final. Seguimos los siguientes pasos:

19. ¿Cuánto debe pagar una persona por concepto de intereses de una deuda por $50,000, si la liquida 2.5 años después, a una razón de 25% anual?
- $12,500
- $20,000
- $31,250
Resolución
Para calcular el monto de los intereses de una deuda utilizando la fórmula del interés simple, seguimos los siguientes pasos:

20. ¿En cuánto tiempo un capital de $18,000 se convierte en $75,000, si la tasa de interés simple que ofrece una institución bancaria es de 41% anual?
- 1.70 años
- 4.16 años
- 7.72 años
Resolución
Para determinar el tiempo necesario para que un capital se convierta en un monto específico a una tasa de interés simple, utilizamos la fórmula del interés simple reorganizada para despejar el tiempo. Sigamos los pasos:

21. ¿Durante cuánto tiempo se ha invertido un capital de $3,500,000 que produjo intereses de $2,600,000 a una tasa anual de 4%?
- 1.34 años
- 2.97 años
- 18.57 años
Resolución
Para calcular el tiempo durante el cual se ha invertido un capital que ha generado una cierta cantidad de intereses a una tasa de interés simple, utilizamos la fórmula del interés simple reorganizada para despejar el tiempo. Veamos cómo se hace:

22. Una persona solicita un préstamo por $60,000 a un plazo de 12 meses. Si en el primer mes paga $8,000 de su deuda y en el doceavo $5,250, ¿cuál es la diferencia entre los pagos que efectúa mensualmente?
- -$250
- -$229
- $250
Resolución
Se nos pide que identifiquemos la diferencia que hay entre los pagos mes con mes cuando el primer mes se paga 8,000 y el doceavo se paga 5,250, entonces tenemos los siguientes datos:
- Pago en el primer mes: $8,000.
- Pago en el doceavo mes: $5,250.
- Plazo del préstamo: 12 meses.
Primero debemos conocer la diferencia entre el primer y ultimo mes.

23. Si una persona desea obtener al finalizar 1 año el monto de $10,000.00, ¿qué cantidad debe depositar hoy en un banco que ofrece una tasa de interés simple de 12% anual?
- $8,928.57
- $10,833.33
- $11,200.00
Resolución
Para determinar cuánto debe depositar una persona hoy para obtener un monto específico al final de un período a una tasa de interés simple, usamos la fórmula del monto simple reorganizada para calcular el capital inicial.

24. Es la ganancia por invertir dinero, es decir, la cantidad que se pagará por este.
- Monto
- Interés
- Capital
Resolución
La descripción proporcionada corresponde al concepto de “Interés”. El interés es la ganancia que se obtiene por invertir dinero o, desde el punto de vista del prestatario, es la cantidad que se paga por el uso del capital. Es una medida de la rentabilidad de una inversión o el costo de un crédito.
Recomendaciones finales
Para aprovechar al máximo este simulador:
- 📌 Responde bajo tiempo límite para acostumbrarte a la presión del examen real.
- 📌 Analiza cada explicación: no memorices, comprende la lógica detrás del resultado.
- 📌 Refuerza los temas débiles: vuelve sobre aquellos en los que más fallas.
- 📌 Haz simulacros completos para entrenar tu resistencia mental y concentración.
- 📌 Apóyate en recursos adicionales: en Pasatuexam encontrarás guías completas, ejemplos resueltos y estrategias que te ahorrarán tiempo y esfuerzo.
Empieza gratis con los temas disponibles, pero si quieres cubrir absolutamente todo y aumentar tus posibilidades de quedar en tu primera opción universitaria, desbloquea el curso completo.
👉 Con Pasatuexam tendrás un plan estructurado, explicaciones paso a paso y la confianza para llegar al EXANI-II preparado al 100%. ¡No dejes pasar la oportunidad de estudiar con ventaja y asegura tu lugar en la universidad de tus sueños!
🚀 ¡Potencia tu Preparación con Nuestro Plan Profesional! 🎓
Si has empezado a descubrir cómo prepararte para el EXANI-II con nuestro contenido gratuito, ¡te felicitamos! 🌟 Pero, ¿estás listo para dar el gran salto? Con nuestro Plan Profesional, no solo vas un paso adelante, ¡vas a volar! 🚀
Al elegir el Plan Profesional, desbloquearás acceso a:
- Contenido sin Publicidad y sin Interrupciones 🚫: Estudia con la máxima concentración, sin anuncios que te distraigan de tus objetivos.
- Contenido de Calidad 100% Basado en las Guías del EXANI-II 📚: Confía en un material que sigue fielmente el currículo oficial, maximizando tu eficacia en el estudio.
- Lecciones Escritas y Videos Explicativos 📝🎥: Visualiza conceptos complejos con materiales diseñados para facilitar tu aprendizaje.
- Explicaciones Paso a Paso 📘: Todo se entiende mejor con nuestros métodos sencillos y claros.
- Preguntas Como en el Examen ❓: Practica con ejercicios que te preparan de verdad, aumentando tu seguridad al máximo.
- Simuladores de Examen 💻: Siente el día del examen antes de llegar, para que nada te sorprenda.
- Acceso Multiplataforma 📱💻: Aprende cuando quieras y desde cualquier dispositivo, facilitando tu preparación en todo momento.
Asegura tu acceso al éxito con el Plan Profesional. No es solo preparación, es tu boleto para lograr tus sueños universitarios. ¡Decídete ya! 🌈 No dejes pasar esta oportunidad. ⏳ ¡El tiempo vuela y tu futuro te espera!
🌟 Simulador Gratis 🌟
Si estás curioso sobre lo que el Plan Profesional puede ofrecerte, te tenemos una sorpresa. Haz clic aquí y enfrenta nuestro simulador especial. Con solo 30 preguntas, podrás medir qué tan preparado estás para tu examen de admisión. 🎯
Esta es tu oportunidad de obtener un vistazo de la calidad y profundidad que nuestro Plan Profesional tiene para ofrecer, y al mismo tiempo, evaluar tu nivel actual de preparación. 💪

